Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 981234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969799100

Enunciado

USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 9c

Calcule as integrais:

c) ∫ ∫ R 1 x 2 + y 2 d x d y , onde R é a região interior à cardioide r = 1 + sin ⁡ θ   e exterior à circunferência r = 1 .

Passo 1

Fala, galera! Vamos resolver essa questão!

O enunciado pediu pra gente calcular a integral dupla ∫ ∫ R 1 x 2 + y 2 d x d y sobre a região R , que é a região interior à cardioide r = 1 + sin ⁡ θ   e exterior à circunferência r = 1 . Seria mais ou menos isso aqui:

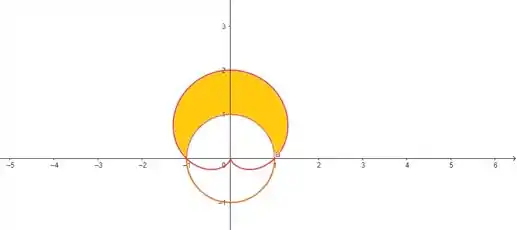
Sempre que a função apresentar algum tipo de simetria rotacional, como é o caso dessa região, é interessante usar as coordenadas polares, porque elas vão facilitar nossos cálculos na hora de integrar. Pra isso, a gente conta com as relações:

x = r cos ⁡ θ

y = r sin ⁡ θ

J = r

Esse J é o nosso Jacobiano e é muito importante não esquecer dele na hora da integral, sempre que fazemos alguma transformação de coordenadas. Mas nesse caso, nossas curvas já estão em coordenadas polares, então a única transformação que vamos fazer é na função do integrando. Além disso, r é o raio das circunferências e θ é o nosso ângulo. Com base nessas equações conseguimos obter nossos intervalos de integração e calcular a integral pedida.

Vamos lá!

Passo 2

Repare que nossa região vai da circunferência r = 1 até o o cardioide em r = 1 + sin ⁡ θ . Assim, temos:

1 ≤ r ≤ 1 + sin ⁡ θ

Pra descobrir como varia nosso ângulo, vamos verificar onde as curvas se intereceptam, pra isso, basta igualar as equações:

1 = 1 + sin ⁡ θ

sin ⁡ θ = 0

Pra que sin ⁡ θ seja igual a 0 , vamos ter θ = 0 ou θ = π . Então, temos nosso intervalo:

0 ≤ θ ≤ π

Assim, usando r = cos ⁡ θ e y = r sin ⁡ θ , no integrando 1 x 2 + y 2 , vamos ter:

1 x 2 + y 2 = 1 r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ = 1 r 2 = 1 r

E conseguimos escrever nossa integral na forma:

∫ ∫ R 1 x 2 + y 2 d x d y = ∫ 0 π ∫ 1 1 + sin ⁡ θ 1 r   r   d r d θ

= ∫ 0 π ∫ 1 1 + sin ⁡ θ 1   d r d θ

Passo 3

Então, integrando primeiro em relação a r , temos:

∫ 0 π r 1 1 + sin ⁡ θ d θ

Aplicando os limites de integração em r :

∫ 0 π 1 + sin ⁡ θ - 1 d θ = ∫ 0 π sin ⁡ θ d θ

Passo 4

Agora integrando em relação a θ , vamos ter:

∫ 0 π sin ⁡ θ d θ = - cos ⁡ θ 0 π

Aplicando os intervalos de integração em θ :

- cos ⁡ π + cos ⁡ 0

Como cos ⁡ ( π ) = - 1 e cos ⁡ 0 = 1 , temos:

- - 1 + 1 = 2

Valeu, galera! Até a próxima! 😉

Resposta

2

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}