USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 37
Se D é a região limitada pelas curvas e e se
Então podemos afirmar que
Passo 1
Olá amigo, tudo bem? Estou aqui hoje para te ajudar a resolver esse problema. O que queremos é encontrar os intervalos de integração, para isso iremos primeiro visualizar as curvas dadas.
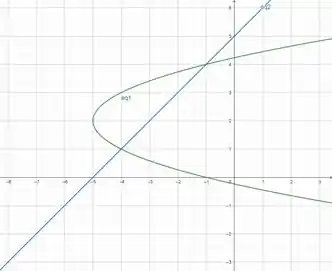
Passo 2
Por termos o gráfico da região já somo ajudados, para encontramos os limites. Os limites a e b são mais fáceis de visualizar, eles são os limites de y, é de onde o começa a passar pela nossa região até onde vai. Podemos ver então que é .
Em relação a x, o que iremos observar é de onde partimos e para onde vamos no sentido vertical, e nesse caso partimos do gráfico azul e vamos para o gráfico verde, isso é
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x