USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 5a
Calcule as seguintes integrais duplas:
a)
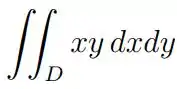
Onde
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para calcular a seguinte integral:
Para resolver ela, primeiro precisamos integrar em relação a e depois em relação a (por conta dos limites de integração) da seguinte forma:
E aí? Bora lá??!!
😉
Passo 2
Assim, primeiro integrando em relação a , temos:
Agora, integrando em relação a , temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x