USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 10b
Esboce a curva e calcule a área da região indicada:
b) a região limitada pela lemniscata
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente esboçar a curva polar e calcular a área da região limitada por essa lemniscata.
O gráfico de uma equação polar consiste em todos os pontos que tem pelo menos uma representação cujas coordenadas satisfaçam a equação. E a área dessa região é dada pela integral dupla:
Onde . Então, vamos descobrir como varia o raio e o ângulo na nossa região para descobrir os nossos intervalos de integração.
Vamos lá!
Passo 2
A curva é uma lemniscata com quatro laços. Com o auxílio de uma ferramente computacional, podemos plotar essa curva no gráfico:
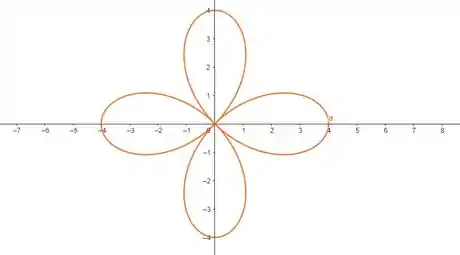
Pra calcular a área total dela, vamos multiplicar área de um laço por . Como cada laço tem um ângulo no intervalo , montando nossa integral, vamos ter:
Passo 3
Então, integrando primeiro em relação a , vamos ter:
Aplicando os limites de integração em :
Passo 4
Antes de integrar em relação a , vamos fazer uma substituição e chamar . Dessa forma, . Além disso, quando , temos . Da mesma forma, quando , temos . Então, substituindo tudo, vamos obter:
Então, integrando em relação a :
Aplicando os intervalos de integração:
Valeu, galera! Até a próxima! 😉