USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 6e
Determine o volume do sólido em cada um dos seguintes casos:
e) é a região do primeiro octante limitada pelo cilindro e pelos planos , e .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o volume do sólido que é limitado no primeiro octante pelo pelo cilindro e pelos planos , e .
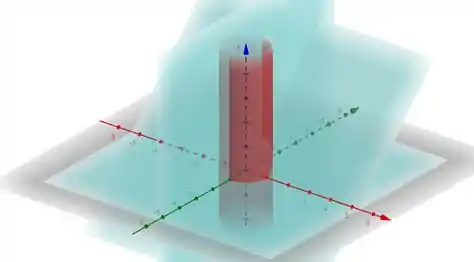
Como o sólido é limitado só no primeiro octante, vamos observar apenas a parte positiva do gráfico e verificar como e estão variando. Assim, a gente consegue encontrar os limites de integração do nosso volume na equação:
Vamos lá!
Passo 2
O enunciado nos diz que nossa região é limitada por e . Então, temos:
Agora repare que a projeção do cilindro no plano é a circunferência de equação :
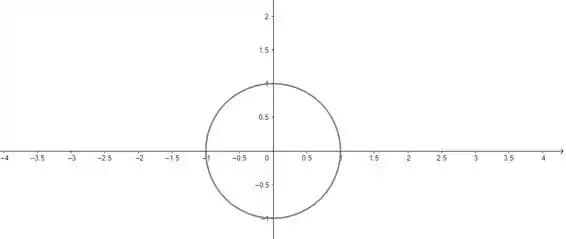
Como a gente quer só a parte positiva e nossa circunferência tem raio , então tá variando de a . Além disso, isolando na equação da circunferência, temos , pegando só a parte positiva, vamos ter:
Passo 3
Agora que já temos nossos intervalos, é só montar a integral de volume:
Integrando primeiro em relação a , temos:
Integrando agora em relação a :
Aplicando os limites de integração em :
Por fim, integrando em relação , vamos obter:
Aplicando os limites em e somando as frações:
Valeu, galera! Até a próxima! 😉