USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 11
Determine o volume da região interior à esfera e exterior ao cilindro , com .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar o volume da região dentro da esfera e fora do cilindro , com . Plotando o cilindro e a esfera, teremos:
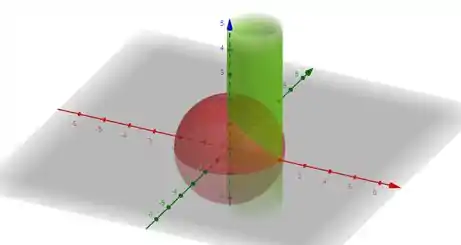
Então, vamos descobrir como , e estão variando dentro da nossa região e em seguida, usar as coordenadas cilíndricas, pra ficar mais fácil de integrar, através das relações:
Vamos lá!
Passo 2
Vamos começar analisando a equação do cilindro , usando :
Mas a gente sabe que , então:
Então, temos o intervalo de variação do raio:
Como a gente quer que seja sempre positivo, vamos pegar o ângulo de variação no intervalo:
E multiplicar por , pra pegar os octantes positivos do espaço tridimensional. Além disso, isolando na equação da esfera, e pegando só a parte positiva, vemos que ele varia como:
Mas como , temos:
Passo 3
Com os nossos intervalos, conseguimos montar a integral:
Então, integrando em relação a :
Pra integrar em relação a , vamos fazer uma substituição e chamar , de modo que:
Substituindo na integral:
Integrando em relação a :
Voltando a nossa variável original, antes de aplicar os intervalos:
Aplicando os limites de integração em :
Assim, integrando em relação a e aplicando os intervalos de integração, vamos ter:
Valeu, galera! Até a próxima! 😉