USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 35
Calcule a massa do sólido limitado por , com sendo a densidade
Passo 1
Olá meu caro amigo, tudo bem com você? Pronto para calcular essa integral? Para calcularmos a massa de um sólido delimitado, precisamos usar uma integração tripla. Antes de tudo é interessante que olhemos para o sólido formado pois assim poderemos entender melhor a região que estamos integrando e isso irá nos ajudar com os intervalos de integração.
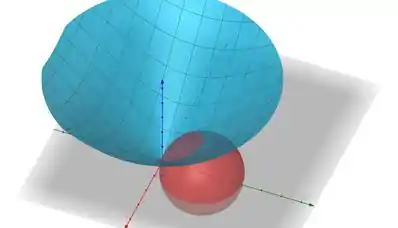
Primeiro estamos acima de
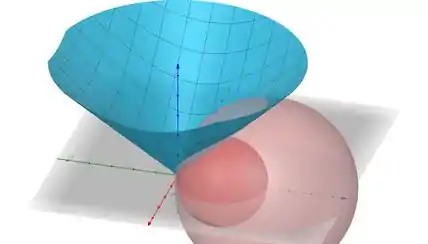
mas estamos abaixo de .
Passo 2
Como estamos trabalhando com esferas, nada mais justo que utilizamos coordenadas esféricas aqui
como
e vamos até pois assim conseguiremos ‘ler’ todo o nosso sólido nesse sentido.
Em relação a a variação é de pois assim conseguiremos ‘ler’ toda circunferência do nosso sólido. O que nos falta encontrar é a variação de . Como somos externos a e internos a .
Então vamos descobrir aqui quais os valores de substituindo os parâmetros nas equações das esferas.
Para a segunda esfera temos
então
Passo 3
Agora vamos montar nossa integral e calcular
Primeiro integramos em relação a e por ser constante sai da integração o resultado
agora em relação a
agora por último em relação a
aplicando uma substituição e mudando os limites de integração