USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 28c
Calcule onde V é o solido limitado por
Passo 1
Olá meu amigo, tudo bem? Pronto para calcular uma integral tripla marota? Espero que sim viu, antes de tudo eu quero te mostrar a região V, importante sempre compreender bem qual é a região que iremos integrar para não erramos nada.
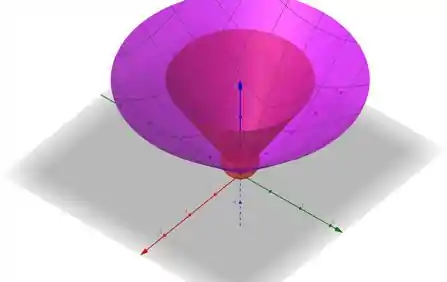
A nossa região está limitada por os cones e dentro da esfera.
Passo 2
Para calcular a integral tripla , onde é o sólido limitado pelas superfícies , e , vamos usar coordenadas esféricas. As coordenadas esféricas são úteis quando lidamos com superfícies esféricas, como a que temos aqui.
As coordenadas esféricas são definidas da seguinte forma:
onde é o raio, é o ângulo polar que varia de 0 a , e é o ângulo azimutal que varia de 0 a .
Vamos começar a calcular a integral na nova base de coordenadas. Primeiro, precisamos encontrar os limites de integração em termos de e .
1. A superfície pode ser reescrita como , o que implica .
2. A superfície corresponde a , o que implica , ou seja, .
3. A superfície corresponde a , o que implica , ou seja, .
Portanto, os limites de integração serão:
Agora, podemos calcular a integral usando coordenadas esféricas. A expressão se torna nas coordenadas esféricas. Portanto, a integral tripla se torna:
Agora, podemos calcular essa integral:
Agora, integramos em relação a :
Se e
Voltando para o cosseno
Agora iremos continuar a nossa integral do volume