USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 29f
Calcule a massa da região R limitada por:
, , para com .
Passo 1
Olá meu caro colega, Yuri aqui e hoje iremos resolver essa querida integral tripla para encontramos a massa de um solido dado. A região que iremos trabalhar é a seguinte
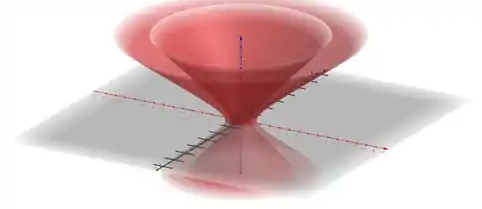
Para que não tenhamos um trauma no calculo dessa integral o melhor a se fazer é parametrizar as equações. Uma parametrização interessante é a
E o querido jacobiano é
Agora é hora de encontramos os intervalos da integral a partir da parametrização
Passo 2
Agora é hora de calcularmos a massa por meio da integral tripla
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x