USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 7
Escreva duas integrais iteradas correspondentes à integral dupla , onde é a região do plano limitada pelas curvas e .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente escrever duas integrais iteradas na forma , sabendo que é a região do plano limitada pelas curvas e .
Plotando essas curvas, nós temos:
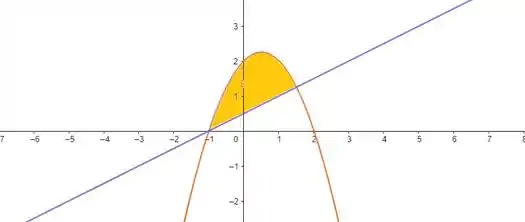
Então, nossa região é essa em amarelo. Nós vamos escrever uma integral iterada e uma integral iterada . Pra isso, a gente precisa definir os intervalos de integração, com base na região dada, e escrever nossa integral dupla.
Vamos lá!
Passo 2
Repare que o é limitado pelos pontos de interseção entre as curvas. Nós encontramos eles, igualando as equações e .
Encontrando as raízes dessa equação do segundo grau, temos e . Então,
E o vai variar entre as curvas, então, temos:
E podemos escrever nossas duas integrais iteradas na forma:
Valeu, galera! Até a próxima! 😉