USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 5e
, onde é a região limitada por
Passo 1
Fala pessoal, tudo certinho com vocês? Vamos para mais uma questão de Cálculo. Dessa vez para calcularmos uma integral
Nosso objetivo é calcular , onde é a região limitada por
Passo 2
Vamos montar nossa integral. Começando pela região. Para melhor entendermos o que está acontecendo. Vamos desenhar a região
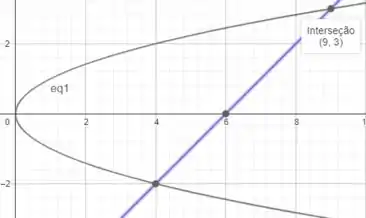
Para esse caso, seria mais fácil integrarmos primeiro em e depois em . Sendo assim, como
portanto
E ao olharmos o gráfico, vemos que
Então a integral fica
resolvendo temos:
Integrando temos:
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento acima
Exercícios de Livros Relacionados
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x