USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 28a
Calcule o volume da região acima do cone e dentro da esfera .
Passo 1
Olá meu caro amigo, como está? Agora iremos calcular o volume de uma região dada, para isso iremos utilizar a integração tripla, mas iremos parametrizar tudo direitinho para que não tenhamos muitos problemas com a integração. Antes de tudo vamos começar visualizando a região que iremos integrar.
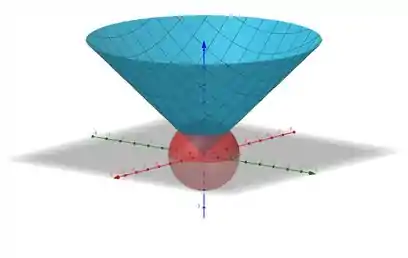
A dita cuja nada mais é do que a região do cone dentro da circunferência, então é um cone com uma cabecinha da circunferência. Uma parametrização adequada é a,
Passo 2
O volume é calculado por
Colocando os limites da integração
Resposta
Exercícios de Livros Relacionados
58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d