Sejam e considere o sistema linear
nas incógnitas reais Considere também as seguintes afirmações:
(I) se são tais que esse sistema possui solução, então o seu conjunto solução será descrito usando no máximo uma variável livre;
(II) esse sistema é impossível para certos valores de ;
(III) se esse sistema tiver infinitas soluções, então .
As afirmações verdadeiras são:
- apenas a 2
- apenas a 1 e 2
- apenas a 1
- apenas a 2 e 3
- apenas a 1 e 3
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é verificar quais afirmações sobre o sistema são verdadeiras
Como todas as afirmações envolvem as soluções desse sistema, talvez seja interessante resolvermos o sistema via escalonamento do sistema aumentado. Bem, então vamos começar construindo o sistema aumentado.

Passo 2
Bem, vamos começar montando a matriz aumentada do nosso sistema. Como o sistema é
A matriz aumentada fica
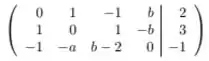
Agora, vamos começar o processo de escalonamento do sistema.
Então fazemos: . Fazendo isso, temos:
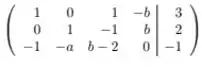
Agora, podemos fazer
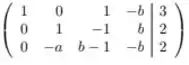
E, por fim, fazemos
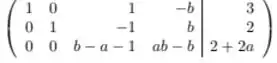
Dessa forma, terminamos nosso escalonamento

Passo 3
Agora podemos checar as afirmações. Vamos começar com a primeira afirmação. Ela diz que
se são tais que esse sistema possui solução, então o seu conjunto solução será descrito usando no máximo uma variável livre;
Vamos pensar, existe alguma condição para nosso sistema ter variáveis livres? Isto é termos apenas equações e incógnitas? Olhando nosso sistema escalonado
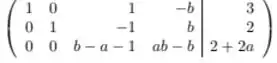
Se a última linha fosse nula, ela não seria relevante para o sistema, ou seja, teríamos equações e incógnitas. E quando essa linha é nula? Quando
Resolvendo esse mini sistema, descobrimos que
Dessa forma, teremos duas variáveis livres no nosso sistema. Logo a primeira afirmação é falsa.
Vamos para a segunda
Passo 4
A segunda afirmação diz que esse sistema é impossível para certos valores de ; E aí? Como fazemos? Bem impossibilidades ocorrem quando temos algo da forma , onde
Então ao olharmos o nosso sistema,
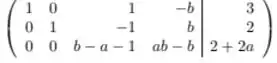
essa impossibilidade aconteceria quando
Ou seja, precisamos que
e
Fazendo , e substituindo na segunda equação
Logo
Assim para , obtemos que o sistema não tem solução. Logo a segunda afirmação é verdadeira quando .

Passo 5
Agora, vamos checar a última afirmação. Ela diz que se esse sistema tiver infinitas soluções, então
Quando temos que a última linha do sistema escalonado fica .
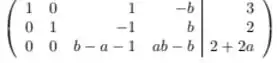
Então, sempre que O sistema tem solução, e terá infinitas porque temos uma variável livre. Portanto, essa afirmação é falsa
Portanto, a única afirmação verdadeira é a segunda. Situação presente na alternativa

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊