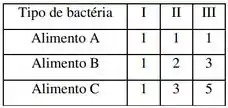
Um biólogo colocou três espécies de bactérias (denotadas por I, II e III) num tubo de ensaio, onde elas serão alimentadas por três fontes diferentes de alimentos (A, B e C). Em cada dia serão colocadas no tubo de ensaio 1500 unidades de A, 3000 unidades de B e 4500 unidades de C. Cada bactéria consome um certo número de unidades de cada alimento por dia, como mostra a tabela. Quantas bactérias podem coexistir no tubo de ensaio de modo a consumir todo o alimento?
Passo 1
Vamos chamarde a bactéria I, a bactéria II e a bactéria III.
Com os valores dados no enunciado e os coeficientes da tabela, construímos o sistema:
Boaa, agora é só resolver esse sistema pra vermos quantas bactérias podemos ter no tubo para consumir todo o alimento hehe
Passo 2
Escrevendo nosso sistema como uma matriz aumentada:
Agora vamos escalonar:
Opa, uma das linhas foi anulada, vamos voltar pro sistema pra ver o que fazemos.
Passo 3
Voltando ao sistema com os novos coeficientes:
Bom, se uma das linhas foi anulada, já sabemos que uma das respostas vai ser um parâmetro.
Escolhendo como parâmetro, vamos isolar na segunda linha e assim teremos
Substituindo na primeira linha:
Então:
Logo, nesse sistema, pode assumir qualquer valor, enquanto e variam em função dele. Temos infinitas soluções :D