Questão discursiva – UFJF – Equações Diferenciais I – Avaliações Moodle – 2022.2 – Questão 1
Considere as seguintes afirmações sobre as séries e
- Considere que . Se a série converge, então a série converge.
- Considere que . Se a série converge, então a série diverge.
- Considere que . Se a série diverge, então a série diverge.
- Considere que . Se a série diverge, então a série converge.
É correto afirmar:
Escolha uma opção:
- Apenas a afirmação (II) é verdadeira
- Apenas a afirmação (IV) é verdadeira
- Apenas a afirmação (III) é verdadeira
- Todas as afirmações são falsas
- Existem exatamente três afirmações verdadeiras
- Todas as afirmações são verdadeiras
- Existem exatamente duas afirmações verdadeiras
- Apenas a afirmação (I) é verdadeira.
Passo 1
Faaaaaala, galera. Tudo tranquilo por aí?? 😊
Bora comigo que vou te ajudar a entender melhor essa questão!!!
Bom, esse enunciado conta pra gente que existem duas séries: a série e .
E dá pra gente quatro afirmações sobre a relação entre os termos gerais das séries dada por
E como essa relação pode nos trazer informações relevantes sobre a convergência ou a divergentes das séries e .
Antes de começarmos a falar sobre a convergência ou a divergência das séries, vamos só destacar aqui alguns pontos importantes sobre a relação:
- Repare que ou seja, a série é completamente positiva, não sendo uma série alternada, por exemplo.
- E ou seja, a série é maior que a série .
Essas condições nos ajudarão a relacionar a condição de convergência ou divergência das séries. Então vamos analisar cada uma das afirmações.
Passo 2
Para fazer a análise vamos usar o teste da comparação entre as séries. A ideia consiste em comparar mesmo a série que queremos estudar a convergência, com uma série que já conhecemos.
Veja o esquema
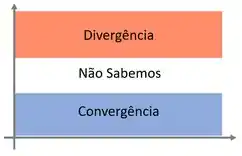
Temos nele três regiões, uma onde podemos localizar as séries que sabemos que convergem, outra onde podemos localizar as séries em que temos certeza sobre a divergência e a região do meio onde poderão ficar as séries em que não podemos afirmar nada sobre a divergência ou convergência.
Vamos agora analisar a primeira afirmação:
- Considere que . Se a série converge, então a série converge.
- Considere que . Se a série converge, então a série diverge.
- Considere que . Se a série diverge, então a série diverge.
- Considere que . Se a série diverge, então a série converge.
Ou seja, podemos localizar a série na região de convergência. Mas a relação nos diz que a série é maior que a série , pois . Então a série estará acima de .
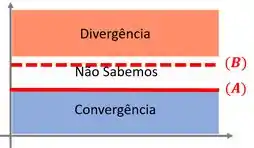
E não podemos ter certeza sobre a convergência ou divergência de . ☹.
Assim, essa afirmação não pode ser necessariamente verdadeira.
Passo 3
Vamos dar uma olhada na segunda afirmação:
E localizando as séries em nossas regiões acontece exatamente o mesmo que no caso anterior:
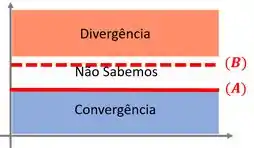
Ou seja, não podemos afirmar nada sobre a divergência de se só sabemos que converge. ☹
E essa afirmação não pode ser necessariamente verdadeira.
Passo 4
Agora vamos analisar a terceira afirmação.
Repare que agora sabemos que a série é divergente, então vamos localizá-la nessa nova região, e sabemos também que a série deverá ficar acima dela.
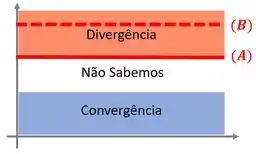
Repare que como a série é maior que a série , e sabemos que a série diverge, podemos afirmar com certeza que a série também divergirá.
E essa é uma afirmação verdadeira 😊.
Passo 5
E para fechar com chave de ouro, vamos analisar nossa quarta e última afirmação.
Ahhh essa é falsa com certeza, porque olha para o esquema:
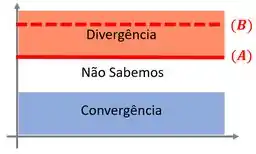
Se é maior que , e é uma série divergente, então não tem nem como ser convergente. Sacou?!!!
E essa é uma afirmação falsa. 😊
Agora que já analisamos tudo, é só marcar a resposta certa e corre para o abraço.
E até a próxima!!!
Resposta
Resposta:
- Apenas a afirmação (III) é verdadeira