3 – Discuta a convergência (diverge ou converge condicionalmente ou converge absolutamente) das séries abaixo:
a)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nesse probleminha, temos que obter a convergência da série e dizer se é divergente ou se é convergente (absolutamente ou condicionalmente).
No caso, a série é dada como
Tem ideia como podemos obter a convergência dessa série?? 🤔🤔
O que acha de aplicarmos o teste da comparação?
Bora ver! 😁
Passo 2
O teste da comparação consiste em comparar a série que queremos analisar com uma série que já sabemos o resultado.
No caso, a série que queremos obter a convergência é dada como e vamos comparar com .
Mas porque essa série? 🤔
Perceba que as séries do tipo são chamadas de p-séries e se for maior que , a série converge, mas se for menor ou igual a , a série diverge.
Portanto possui menor que , logo diverge!
Dessa forma, pelo teste da comparação, se for maior que , certamente diverge, já que se que é menor diverge, uma série maior deve divergir.
Entendeu? 😎
Passo 3
Comparando com , temos
No caso, é ou , mas ainda não sabemos
Mas sabemos que varia entre e como podemos ver no gráfico de .
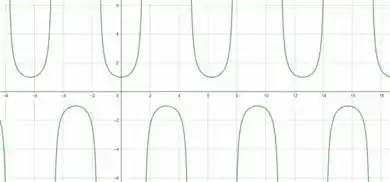
Com isso, podemos afirmar que , ou seja, reescrevendo como
Logo, vemos que
Portanto , com isso, se diverge, certamente também diverge!
É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta
diverge.