UFCG, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - UAMat - Lista 4, Questão 8i
Determine se a série converge ou diverge.
i)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar se a séria converge ou diverge.
A gente poderia pensar em usar o teste da divergência para verificar isso, mas ele não ajudaria muito, porque e nesse caso o teste seria inconclusivo.
Mas a gente pode pensar em comparar essa série com outra que a gente já conheça o comportamento, como a série harmônica:
Assim, vamos usar o teste da comparação, que nos diz que dadas duas séries de termos positivos e :
Vamos lá!
Passo 2
Nossa série é dada por:
Vamos chamar o nosso termo geral :
Agora vamos comparar esse termo com a série geométrica, que tem como termo geral:
Vamos dar uma olhada no gráfico dessas dua funções:
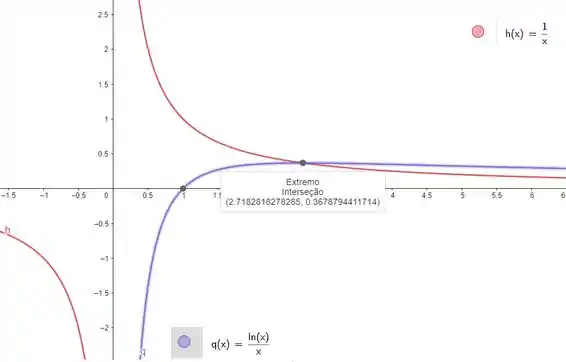
Repare que para começando em , nós temos:
Além disso, nós sabemos que a série harmônica é sempre divergente. Dessa forma, temos:
Então, de acordo com o teste da comparação, também vai divergir e temos:
Valeu, galera! Até a próxima! 😉