UFCG - Sem Campus - Cálculo Diferencial e Integral I - Provas - Teste 9 - AV1 - 2018.1 - Questão 3
Dada a função definida por
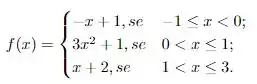
Estude a continuidade de em . Defina em de modo a tornar contínua neste ponto.
Passo 1
Oiiie, tudo bem com você?
Temos uma função que é particionada em três intervalos definidos da seguinte maneira
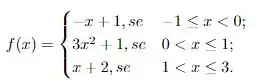
E o enunciado quer que analisemos a continuidade desta função quando . Além disso, o enunciado pede que nós mudemos esta definição acima para que a função seja contínua em . Okay, mas como podemos fazer isso? A continuidade de uma função pode ser vista como a possibilidade de desenhar o gráfico desta função sem tirar o seu lápis do papel em nenhum momento. Mas e matematicamente, é possível mostrar que isso acontece?
Se você seguir o gráfico de uma função contínua, não importa de qual lado (esquerdo ou direito) você comece a desenhar a função, você passará pelos mesmos pontos, se ela for contínua nestes pontos. Em particular, se queremos checar se ela é contínua em , é preciso que não importando de que lado estamos desenhando a função, a gente passe por este ponto, sem tirar o lápis do papel. O que se traduz na igualdade dos limites laterais
que é o limite pela direita, e
que é o limite pela esquerda! Se os limites existem e são iguais, a função é contínua em , então bora lá!
Passo 2
Vamos começar com o limite pela direita, ou seja, vamos calcular
Se estamos analisando a função vindo pela direita de , então estamos usando valores de maiores que 1, , neste intervalo temos que nossa função é
Utilizando isso em nosso limite, e avaliando quando , temos que
Ou seja, temos que
Agora, precisamos verificar o limite pela esquerda! O processo é análogo ao que fizemos neste passo! Vem comigo!
Passo 3
O limite pela esquerda, ou seja
Mas, como estamos vindo pela esquerda de , estamos pegando valores menores que , . O intervalo da função mais próximo de pela esquerda é o intervalo , em que a função é definida como
Utilizando esta definição em nosso limite, e avaliando quando , temos que
Que resulta em
Como temos que
Temos que função é descontínua em . Beleza! Isso é a primeira parte do problema resolvida! Agora vamos só finalizar com a análise para garantir a continuidade em . Consegue enxergar quando isso acontece?
Passo 4
Saca só! Nós queremos que a função
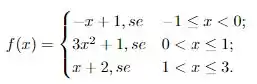
Seja contínua em , da mesma forma que fizemos nos passos anteriores, precisamos analisar os limites laterais, mas agora em torno de , aqui nós temos que pela direita, ou seja, valores poucos maiores que , a função é definida como
e, o limite pela direita é tal que
em que avaliei o limite em , resultando em
Analogamente, podemos fazer o processo pela esquerda, ou seja, valores um pouco menores que , a função neste intervalo é definida como
e, o limite lateral é
de forma que temos que
Como temos que
Então a função é contínua em se fizermos apenas uma pequena modificação em nossa definição, note que os intervalos são e . Ou seja, ela não tem valor exatamente em . Adicionando uma igualdade em qualquer um dos intervalos, garantimos a continuidade de nossa função!
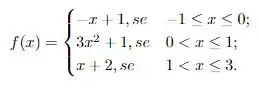
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!