UFF, Cálculo IA-Lista 3, GMA, 2008-1, Questão 14
Verifique se a função dada é contínua nos pontos indicados. Justifique a resposta.
Onde é a função maior inteiro que não supera . Nos pontos e
Sugestão: Esboce o gráfico de
Passo 1
Antes de começar a resolver a questão, vamos falar desse tal de maior inteiro que não supera , o tal de . Apesar de diferente, não tem nada de muito complicado com ele. Se temos , por exemplo, então:
Que é o maior inteiro que não é maior que . Veja que esse valor de é válido para todo o intervalo , levando:
Nesse intervalo. Seguindo esse princípio, temos que:
Para .
Para .
Para
Como faz parte do intervalo proposto na questão e não supera , temos que:
Para . Isso tudo resulta na função chaveada:
Passo 2
Vamos agora, esboçar o gráfico da função. Apesar de termos muitas expressões, temos somente retas, o que acaba compensando.
Vamos esboçar os gráficos como se não houvesse intervalo e depois vamos aplica-los.
A reta tem zero em:
E corta o eixo em:
Da mesma forma, para :
E, para :
Ligando os pontos, chegamos a:
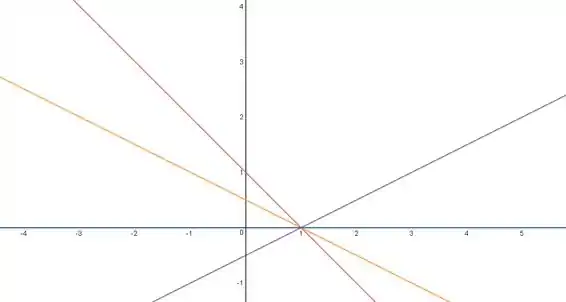
Com em vermelho, em laranja, em azul e em roxo. Veja que as retas se encontram todas em .
Passo 3
Vamos agora aplicar os limites de cada intervalo. A expressão em vermelho é válida para . Como temos o sinal de menor ou igual em , marcamos com bolinha de recheio preto nesse ponto. Onde não há igual, deixamos uma bolinha de recheio branco.
Seguindo a ideia para as demais expressões, chegamos a:
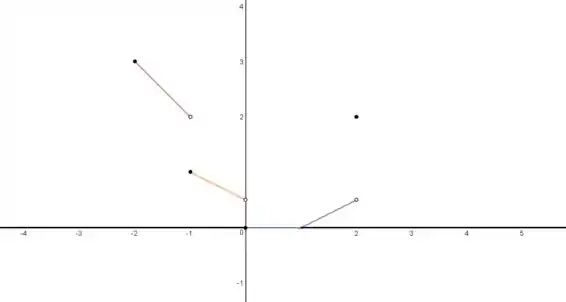
Passo 4
Uma vez com o gráfico, nem precisamos calcular limites aqui. Veja que a há saltos em , e , logo a função não será continua nesses pontos.
Resposta
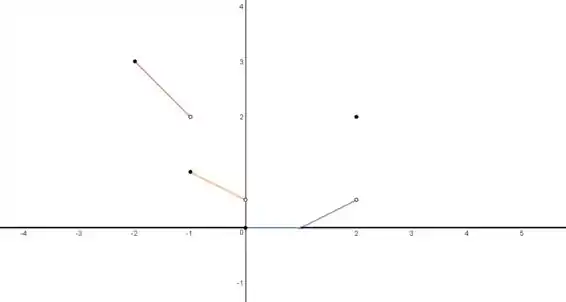
É contínua em e descontínua em .