UNICAMP – Cálculo 1 – Provas Antigas – P1 – 2022.1 - 6ª Diurno – Questão 5
Mostre que existe um número real que é igual a soma de seu cubo e de seu quadrado menos cinco.
Passo 1
Eaee, belezinha?? Vamos primeiro colocar em termos matemáticos o que a questão nos diz, ou seja, queremos um número de tal forma que:
Em que .
Sabendo disso, podemos passar o para o outro lado da igualdade, de forma que criamos a seguinte função:
Passo 2
Plotando o gráfico de , temos:
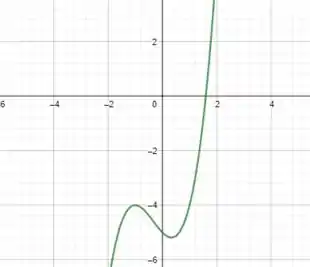
Note que no intervalo existe o zero da função, em que retorna para a equação que a questão nos deu, ou seja:
Assim, podemos concluir que há um número real dentro do intervalo que é igual a soma de seu cubo e de seu quadrado menos cinco.
Entendeu direitinho? Responde aee ;)
Resposta
Resolução no texto
Exercícios de Livros Relacionados
Explique por que a função é descontínua no dado número a . Esboce o gráfico da função. f x = x 2 - x x 2 - 1 , x ≠ 1 1 , x = 1 ,a = 1
Localize as descontinuidades da função e ilustre com um gráfico. y = ln t g 2 x
Explique, usando os teoremos 4, 5, 7 e 9, por que a função é contínua em todo número em seu domínio. Diga o domínio. R x = x 2 + 2 x - 1
Use a definição de continuidade e propriedades dos limites para demonstrar que a função é contínua em um dado número a . f x = x 2 + 7 - x , em a = 4 .
Explique, usando os teoremos 4, 5, 7 e 9, por que a função é contínua em todo número em seu domínio. Diga o domínio. F x = s e n - 1 ( x 2 - 1 )