Considere a função definida pelo gráfico abaixo.

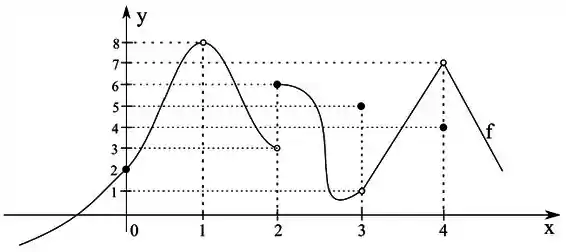
1. Determine o para se existir
2. Em que ponto não é contínua

Vamos ver agora quando

Também vemos isso pelo gráfico

Vamos ver agora quando , repara que dessa vez se olharmos valores menores que o limite vai ser , ou seja, o limite lateral pela direita vai ser

Agora se olharmos valores maiores que o limite vai ser , ou seja, o limite lateral pela direita vai ser

Como os limites laterais são diferentes, esse limite não existe.

Vamos agora para o ponto , se liga que o valor da função em vai ser , que é onde está a bolinha preta, mas o seu limite não é esse, o limite é o valor que a função se aproxima, então é a parte da bolinha aberta, ou seja,

Sacou? Sempre olha o gráfico da função perto do ponto e não necessariamente no ponto, a mesma coisa vai acontece se pegarmos , o valor da função vai ser enquanto o limite vai ser a parte da bolinha branca, ou seja, .

A primeira coisa é o limite precisar existir, e já vimos no item que o limite quando não existe, então a função não vai ser contínua nesse ponto.

Agora temos que ver quando o limite no ponto é igual a função, vimos no passo que nem e nem vão ter o limite igual aos valores do ponto, então já temos mais dois pontos que não são contínuas.

Se olharmos não vai ter valor para a função nesse ponto, porque afinal não tem bolinha fechada em lugar nenhum com então não é continua ali também.

Em podemos ver que a bolinha fechada está exatamente em cima da função então o limite vai ser igual ao valor da função no ponto.

Conclusão, os pontos que a função não é continua são: