Considere a função definida por
O valor de para que seja contínua em é:
Passo 1
Definir a condição para uma função ser contínua
Beleza, antes de mais nada, vamos lembrar: quando mesmo que uma função é contínua? Saca só:
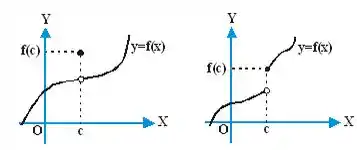
Então pra ficar bem claro, a gente pode entender as funções contínuas como funções em que a gente não tira o lápis do papel pra desenhar. Pra nossa querida e amada poder ser desenhada assim, seja:
Vamos ter que fazer:
Passo 2
Resolver a condição de continuidade
Show de bola, vamos lá. Primeira coisa pra se fazer é substituir
E agora aplicar o :
Opa, problema aí: ? Isso não pode! Vamos então reescrever da seguinte forma:
Ficaremos então com:
E agora sim podemos substituir , saca só:
Resposta
Exercícios de Livros Relacionados
Explique por que a função é descontínua no dado número a . Esboce o gráfico da função. f x = x 2 - x x 2 - 1 , x ≠ 1 1 , x = 1 ,a = 1
Localize as descontinuidades da função e ilustre com um gráfico. y = ln t g 2 x
Explique, usando os teoremos 4, 5, 7 e 9, por que a função é contínua em todo número em seu domínio. Diga o domínio. R x = x 2 + 2 x - 1
Use a definição de continuidade e propriedades dos limites para demonstrar que a função é contínua em um dado número a . f x = x 2 + 7 - x , em a = 4 .
Explique, usando os teoremos 4, 5, 7 e 9, por que a função é contínua em todo número em seu domínio. Diga o domínio. F x = s e n - 1 ( x 2 - 1 )