Considere a função dada por
![]()
a) Construa o gráfico de .
Passo 1
Oiiii pessoal! Tudo bem com vocês? Espero que sim.
Pois bora fazer uma questãozinha de prova?
Bom, vamos analisar primeiro o que a questão nos dá de informação e o que ela deseja, certo?

Então, a questão é sobre uma função que possui seu domínio e a sua imagem no conjunto dos números reais. Além disso, sabemos também que a nossa função muda de “cara” em determinados intervalos, assim, esse entendimento é fundamental para a construção do gráfico.
Passo 2
Bora botar a mão na massa?
Como já mencionado anteriormente, a função em determinados intervalos muda de rosto. Logo, vamos fazer o gráfico da função por intervalos.
Quando o , temos que . Podemos notar com essa função é semelhante a função genérica de uma reta . Logo já sabemos que uma parte do nosso gráfico será uma reta crescente.
Mas deixa eu te falar uma coisa, caso você não tenha acertado de primeira que essa função descreve uma reta, pode simplesmente fazer a tabelinha de valores e depois organizar tudo no plano cartesiano.
Logo, o gráfico para esse intervalo será a reta:
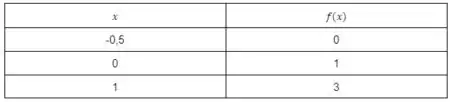
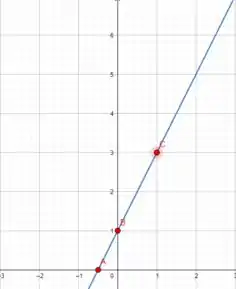
Passo 3
Vamos fazer as mesmas coisas do passo anterior, mas agora para . Nesse intervalo a nossa função será . Como nossa função para esse intervalo é do tipo h(x) = ax²+ bx + c dizemos que nossa função é quadrática, ou seja, seu gráfico será uma parábola com a concavidade voltada para cima.
Então vamos novamente fazer uma tabelinha para em seguida traçar o gráfico:
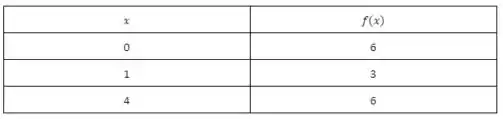
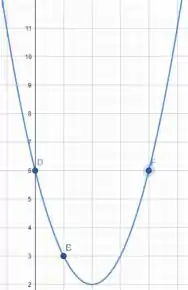
Passo 4
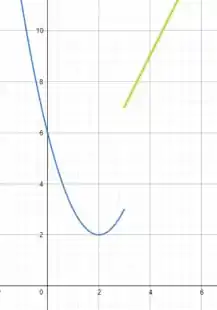
Bom, agora basta que juntemos os dois gráficos respeitando os intervalos de cada das funções e dessa forma teremos o nosso gráfico final.
Desse modo, quando o a função será uma parábola. Já quando o a função terá o formato de uma reta.
E aí? Essa resolução te ajudou?!
Bons Estudos! :)
Resposta
Resolução nos passos acima ;)