Esboce os gráficos e verifique se as seguintes funções são contínuas em cada um dos pontos de
seus respectivos domínios. Justifique suas respostas:
f) dada por:
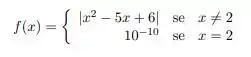
Passo 1
Oii gente linda, tudo bem com vocês?? Bora pra mais uma? Bom, nossa questãozinha quer que esbocemos o gráfico de uma função por partes e que em seguida verifiquemos se a nossa função em questão é contínua. A nossa função é uma função com domínio e imagem no conjunto dos números reais. Não só mas também, a função é uma função por partes, ou seja, para cada intervalo no domínio a função muda de aspecto. E agora?? Como fazemos o gráfico??
Como a função é definida por partes, iremos também fazer o esboço do gráfico por partes.

Passo 2
A nossa função é uma função com domínio e imagem no conjunto dos números reais. Não só mas também, a função é uma função por partes, ou seja, para cada intervalo no domínio a função muda de “cara”. E agora?? Como fazemos o gráfico??
Como a função é definida por partes, iremos também fazer o esboço do gráfico por partes.

Passo 3
Passo 4
Como já tiveram um tempinho para pensar em como construir o gráfico, agora faremos juntinhoss!!! Como já mencionado no passo anterior vamos fazer o gráfico de acordo com os intervalos da nossa função, ou seja, para temos que a função se comporta como . Assim, visualmente já é possível perceber que se trata de uma função modular, justo pela presença do módulo. Logo, já imagina-se que o gráfico para este intervalo não possui imagens negativas. Além disso, temos que dentro do módulo há uma função quadrática do tipo . Em síntese, o gráfico será uma” parábola refletida” e destaca-se que essa parábola não irá passar pelo eixo negativo.
Para nos auxiliar na construção do gráfico utilizaremos uma tabela suporte:
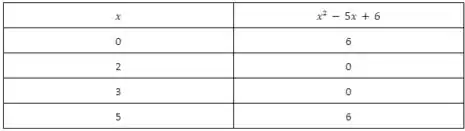
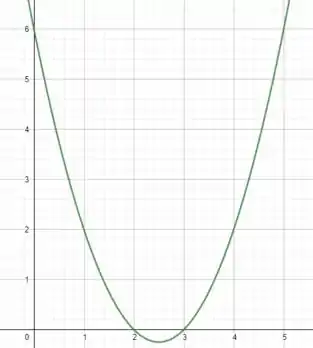
Como eu disse ao ligar as coordenadas cartesianas teremos uma função quadrática , más queremos o módulo dessa função, ou seja, . Então é como se tivéssemos um espelho no eixo x, e a nossa função quadrática fosse um feixe de luz.
Assim, que a feixe de luz encontra o espelho sofre reflexão mudando dessa forma sua direção e sentido. Portanto, a trajetória da luz será como o esboço do nosso gráfico para esse intervalo.
Passo 5
Agora iremos fazer o mesmo passo a passo anterior.
Segundo para o intervalo onde . Trata-se de uma função constante.
A função em questão é: .
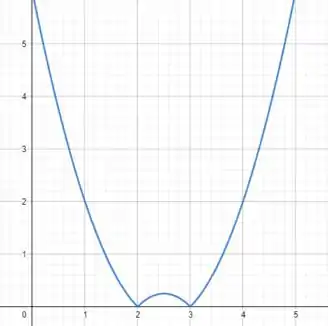
Assim, o gráfico final terá esse aspecto:
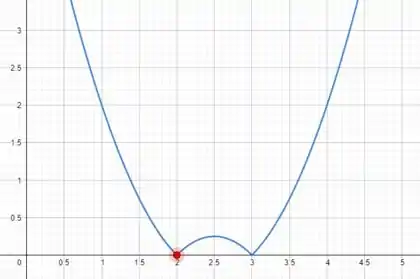
Passo 6
E em relação a continuidade? Vocês acham que essa função é contínua ou não???
Uma função é contínua num ponto de seu domínio quando . Quando é contínua em cada ponto de seu domínio, dizemos que é contínua.
Assim, sabemos que o domínio de são os números reais e pelo gráfico esboçado no passo anterior, vemos que para cada ponto do domínio de existe um . Até mesmo quando o , temos que a função se aproxima do valor por ambos os lados. Portanto, a função é contínua.
outro modo:
Uma forma mais simples e menos “formal” de verificar que essa função é contínua é o fato de gráfico ser contínuo. Em síntese, não tem espacinhos no gráfico. Simples né???
E aí? Essa resolução te ajudou? Responde Aí!

Bons Estudos!
Resposta
Resolução nos passos acima