Esboce os gráficos e verifique se as seguintes funções são contínuas em cada um dos seus respectivos domínios. Justifique suas respostas:
d) dada por
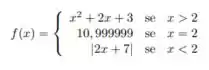
Passo 1
Olá pessoal lindo do Responde Aí, tudo bem? Essa questão parece complicada, mas vou ajudar você aqui! Vamos começar?
A nossa questão deseja que esbocemos o gráfico da função e além disso, faça a verificação se essa função é contínua ou não em relação ao seu domínio. Bom, a nossa função é uma função com domínio e imagem no conjunto dos números reais. Não só mas também, a função é uma função por partes, ou seja, para cada intervalo no domínio a função muda de “cara”. E agora?? Como fazemos o gráfico??
Como a função é definida por partes, iremos também fazer o esboço do gráfico por partes.

Passo 2
Como vocês já pensaram em alguns jeitos de construir o gráfico da função, vamos para a estratégia que eu pensei. Particularmente gosto de fazer o uso de uma tabela para nos auxiliar com os valores do gráfico, bora lá!!!
Primeiro para o intervalo onde : Trata-se de uma função do primeiro grau, ou seja, é do tipo .
A função em questão é:
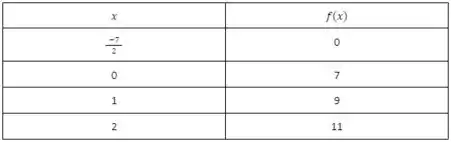
Lembrando que não há uma regra específica de que valores precisamos colocar na tabela, basicamente coloco valores aleatórios apenas para ter noção de como se comporta o gráfico. E que o gráfico dessa questão trata-se também de uma função modular, logo não haverá imagens negativas para esse intervalo.
Construindo o gráfico…
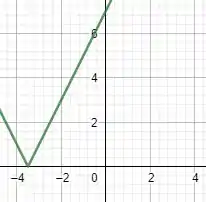
Passo 3
Agora iremos fazer o mesmo passo a passo anterior.
Segundo para o intervalo onde . Trata-se de uma função constante.
A função em questão é:
Passo 4
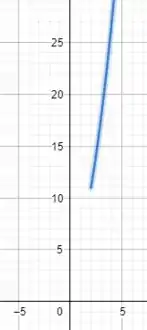
E por fim, seguiremos fazendo o mesmo passo a passo só que agora para o intervalo . Trata-se de uma função do segundo grau, ou seja, é do tipo .
A função em questão é:
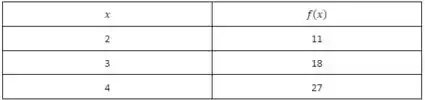
E o esboço para esse intervalo será:
Passo 5
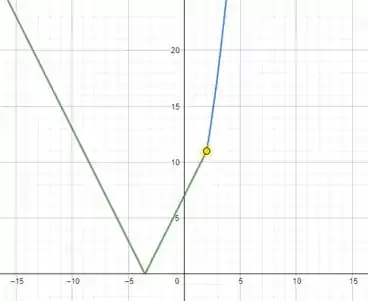
Assim, o gráfico final fica com essa aparência:
Passo 6
E em relação a continuidade? Vocês acham que essa função é contínua ou não???
Uma função é contínua num ponto de seu domínio quando . Quando é contínua em cada ponto de seu domínio, dizemos que é contínua.
Assim, sabemos que o domínio de são os números reais e pelo gráfico esboçado no passo anterior, vemos que para cada ponto do domínio de existe um . Até mesmo quando o , temos que a função se aproxima do valor por ambos os lados. Portanto, a função é contínua.
Resposta
Resolução nos passos acima