Considere a função dada por
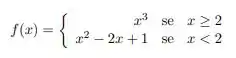
Passo 1
a) Construa o gráfico de f;
Passo 2
Olá pessoal!!! Como vai a vida? Espero que esteja bem!
Prontos pra mais uma questão?
Bom, o enunciado nos diz que a função é uma função com o domínio e contradomínio contidos no conjunto dos números reais. Além disso, o enunciado define como uma função definida por partes, ou seja, a função muda de “cara” de acordo com cada intervalo. Assim, para construir o gráfico dessa função é necessário que cada uma de suas partes seja analisada separadamente.
Passo 3
Como já dito anteriormente vamos construir o gráfico por partes. Primeiro iremos desenhar o gráfico para quando o . Quando o a função é dada por , como essa função possui semelhanças com a função genérica , com .Dizemos então que a nossa função para esse intervalo é uma função quadrática. Portanto, o esboço para esse intervalo será uma parábola.

Na tabela, atribuímos valores ao e obtemos os valores correspondentes na função. Com isso, conseguiremos fazer o traço do gráfico a partir dos pares ordenados obtidos.
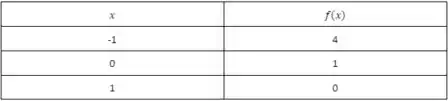
Logo, o gráfico para esse intervalo será:
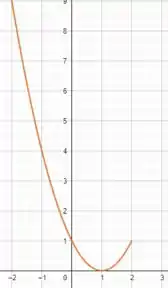
Passo 4
Agora, vamos fazer os mesmos passos acima só que agora para o intervalo , nesse intervalo a nossa função é dada por . Devido ao grau , a função nesse intervalo é nomeada de função cúbica. Para esboçarmos o gráfico desse intervalo utilizaremos novamente o recurso da tabelinha.
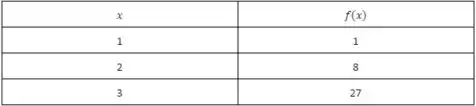
Assim, o esboço para esse intervalo será:
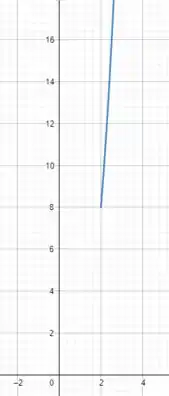
Passo 5
Juntando os esboços anteriores, encontraremos o gráfico final de nossa função. Desse modo, o gráfico terá esse formato :
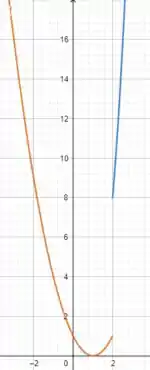
Belezinha? Pois bora continuar praticando!
Bons Estudos!
Resposta
Resolução nos passos acima