Uma espira quadrada de lado gira no sentido horário com velocidade angular em torno do eixo (que contém seu centro), numa região do espaço onde existe um campo magnético:
Onde .
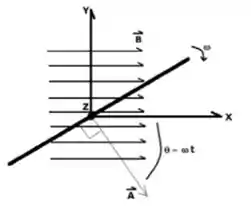
A figura abaixo mostra uma vista superior da espira em rotação com velocidade . Observe que no instante a espira está contida no plano .
Num certo instante de o vetor de área faz um ângulo com o eixo .
Calcule o fluxo magnético na espira quando .
Sabendo que a espira tem uma resistência elétrica de , calcule o valor da corrente induzida na espira no instante .
Suponha agora que o campo magnético comece a variar no tempo, de forma que:
Onde é igual à velocidade angular de rotação da espira.
Nestas condições. Calcule a frequência angular da corrente induzida.
[Sugestão: use a identidade trigonométrica ].
Passo 1
Para determinar o fluxo magnético na espira, precisamos relembrar sua definição:
Onde é o ângulo entre os vetores. Substituindo:
Lembrando que o ângulo está dado em radianos:
Passo 2
Para determinar o valor da corrente, vamos usar a linda Lady Farady!
Como , subsutituindo:
Para o fluxo, temos:
Substituindo na equação da corrente e derivando em relação ao tempo:
Agora é só substituir os valores dados!
Passo 3
Para determinar a frequência angular da corrente induzida, vamos fazer o mesmo mimimi do item anterior, só fica ligado que agora, o campo magnético mudou! Pela Lei de Faraday, temos:
Como , subsutituindo:
Para o novo fluxo, temos:
Substituindo na equação da corrente:
Derivando em relação ao tempo:
Usando a identidade trigonométrica sugerida, temos:
Portanto, a frequência angular da corrente induzida é !
Resposta