Passo 1
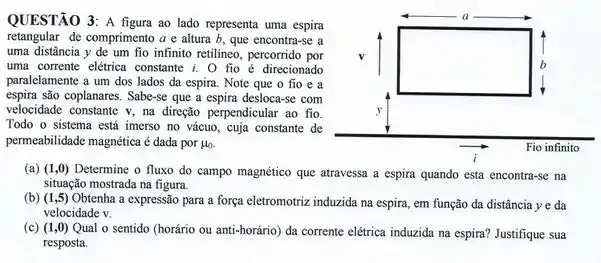
Letra (a). O campo gerado pelo fio varia quando aumentamos ou diminuimos o valor de . Esse valor de campo pode ser determinado pela lei de Faraday:
Para encontrar o fluxo total temos que integrar esse campo com:
E calcular o fluxo em cada pedaço circunscrito pela espira:
Passo 2
Letra (b)
A força eletromotriz pode ser encontrar derivando-se o fluxo magnético em função do tempo. Podemos fazar isso pela regra da cadeia e sabendo que:
Vamos lá:
Passo 3
Letra (c). Pela lei de Lenz, a força eletromotriz induzida tende a surgir num sentido que tende a minimizar a variação de campo magnético. Por isso ela surge no sentido anti-horário.
Resposta
Letra (a).
Letra (b).
Letra (c).
Anti-horário
Exercícios de Livros Relacionados
Quando a corrente em uma bobina de 8 H é igual a 3 A e aumenta para 200 A / s , determine a O fluxo magnético através da bobina e ( b ) a força eletromotriz induzida na bobina.
Determine o fluxo magnético através de um solenoide de 400 voltas que tem comprimento igual a 25,0c m , raio igual a 1,00c m e conduz uma corrente de 3,00 A .
Determine o fluxo magnético através de um solenoide de 800 voltas que tem comprimento igual a 30,0c m , raio igual a 1,00c m e conduz uma corrente de 2,00 A .
Um condutor cilíndrico longo com raio R e comprimento L conduz uma corrente I . Determine o fluxo magnético por unidade de comprimento através da área indicada na Figura 28-44.
44- Variação no campo magnético. Você está testando um novo sistema de captura de dados. Esse sistema permite registrar um gráfico da corrente em um circuito em função do tempo. Como parte do teste, v