Um bastão retilíneo, de comprimento , massa e resistência , desliza, sem atrito, sobre um fio (rígido) condutor ideal (sem resistência), em forma de . O sistema todo está completamente imerso em uma região de campo magnético constante (estacionário e uniforme), perpendicular ao plano que contém o sistema. Inicialmente, uma força externa é aplicada e o bastão move-se com uma velocidade constante para a direita. A partir do instante , essa força externa deixa de agir e o bastão passa a mover-se apenas sob a ação da força magnética, com velocidade . Despreza a capacitância e a autoindutância do sistema, assim como a corrente de deslocamento.
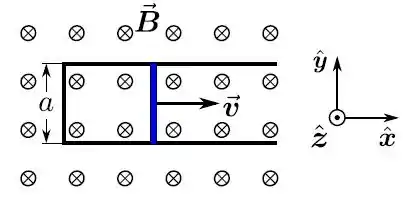
- Qual é o módulo da força eletromotriz induzida no circuito (fio + bastão)?
- Qual é o módulo da (intensidade de) corrente elétrica que passa pelo bastão?
Passo 1
A força eletromotriz pode ser calculada pela Lei de Faraday:
Precisamos calcular a taxa de variação do fluxo magnético. O fluxo é dado pela fórmula:
O campo pode ser escrito, de acordo com o enunciado, pela expressão:
Onde é uma constante positiva. Arbitremos nossa área no sentido positivo de . Portanto, o produto escalar fica:
Substituindo da fórmula, puxamos a constante para fora:
Que resulta na área do retângulo de dimensões:
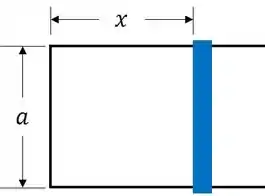
Portanto, o fluxo é:
Onde é uma função do tempo, pois a barra se move.
Passo 2
Substituindo na Lei de Faraday:
Puxando as constantes pra fora derivamos com respeito ao tempo:
Que é a conhecida expressão do módulo da velocidade:
Passo 3
Em seguida, gostaríamos de calcular a intensidade da corrente. Como sabemos que o circuito tem resistência , pela Lei de Ohm:
Logo:
Resposta
a)
b)