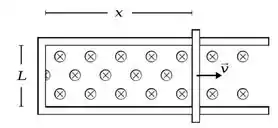
12 - Uma haste com resistência repousa sobre trilhos condutores sem atrito em um campo magnético uniforme constante , como mostrado. Suponha que os trilhos tenham resistência desprezível. A magnitude da força que deve ser aplicada por uma pessoa para puxar a haste para a direita a velocidade constante é:
Passo 1
Bem, a haste possui elétrons livres (cargas).
Se ela tiver parada, os elétrons estarão parados então nenhuma força magnética agirá sobre ele.
Mas se colocarmos a haste em movimento com velocidade , os elétrons vão ter uma velocidade também (formando uma corrente ). A força então pode ser escrita assim:
Agora temos que buscar uma forma de eliminar essa corrente daí!
Passo 2
Bem, sabemos que pela Lei de Ohm...
Onde é a força eletromotriz que surge com a corrente na barra de resistência .
A força eletromotriz também pode ser dada pela Lei de Lenz:
Como estamos trabalhando com a corrente sendo o movimento de cargas negativas...
Onde é a variação de fluxo magnético:
Onde é para o fluxo final e inicial. Ora, o Fluxo inicial era de onde é a área inicial do retângulo .
Como no nosso problema, a variação de fluxo ocorre por um aumento na área do retângulo:
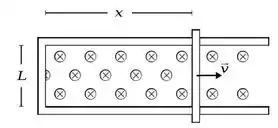
O fluxo final vai ser onde é a variação do deslocamento. Então...
Bem, é a velocidade do trilho, então...
Junto com a lei de Ohm...
Passo 3
Podemos então concluir sobre a força que deve ser feita no trilho para ele se mover com velocidade :
Resposta
Letra D.