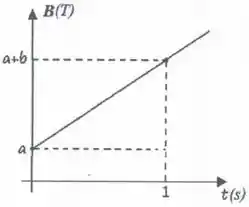
Um conjunto de espiras de cobre circulares de raio se situa num plano perpendicular a um campo magnético dependente do tempo. A variação do campo com o tempo é representada no gráfico. Qual o valor da fem induzida nesta espira?
(a)
(b)
(c)
(d)
(e)
Passo 1
O fluxo magnético através de uma espira é calculado como:
Sabemos que a fem induzida é dada por:
Passo 2
A partir do gráfico dado no enunciado, podemos concluir que
Logo,
Resposta
(b)
Exercícios de Livros Relacionados
Quando a corrente em uma bobina de 8 H é igual a 3 A e aumenta para 200 A / s , determine a O fluxo magnético através da bobina e ( b ) a força eletromotriz induzida na bobina.
Determine o fluxo magnético através de um solenoide de 400 voltas que tem comprimento igual a 25,0c m , raio igual a 1,00c m e conduz uma corrente de 3,00 A .
Determine o fluxo magnético através de um solenoide de 800 voltas que tem comprimento igual a 30,0c m , raio igual a 1,00c m e conduz uma corrente de 2,00 A .
Um condutor cilíndrico longo com raio R e comprimento L conduz uma corrente I . Determine o fluxo magnético por unidade de comprimento através da área indicada na Figura 28-44.
44- Variação no campo magnético. Você está testando um novo sistema de captura de dados. Esse sistema permite registrar um gráfico da corrente em um circuito em função do tempo. Como parte do teste, v