Passo 1
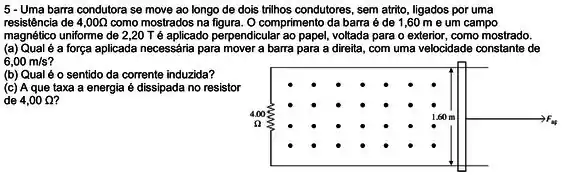
Letra (a). A força pode ser calculada pela fórmula do BILL:
E a força eletromotriz induzida por ser determinada pela lei de Faraday-Lenz:
Onde é a largura da espira em determinado instante e é o comprimento de . Derivando em relação ao tempo achamos a força eletromotriz:
Mas, isolando na equação do BILL:
Substituindo na equação da variação de fluxo:
Passo 2
Letra (b). A corrente induzida surge no sentido a gerar a um campo magnético que se oponha à variação sofrida. Assim, a corrente surge no sentido horário, como podemos confirmar pela regra da mão direita.
Passo 3
Letra (c). Finalmente, para determinar a potência precisamos determinar, antes de tudo, a força eletromotriz:
Logo:
Resposta
(a)
(b) Sentido horário
(c)
Exercícios de Livros Relacionados
Quando a corrente em uma bobina de 8 H é igual a 3 A e aumenta para 200 A / s , determine a O fluxo magnético através da bobina e ( b ) a força eletromotriz induzida na bobina.
Determine o fluxo magnético através de um solenoide de 400 voltas que tem comprimento igual a 25,0c m , raio igual a 1,00c m e conduz uma corrente de 3,00 A .
Determine o fluxo magnético através de um solenoide de 800 voltas que tem comprimento igual a 30,0c m , raio igual a 1,00c m e conduz uma corrente de 2,00 A .
Um condutor cilíndrico longo com raio R e comprimento L conduz uma corrente I . Determine o fluxo magnético por unidade de comprimento através da área indicada na Figura 28-44.
44- Variação no campo magnético. Você está testando um novo sistema de captura de dados. Esse sistema permite registrar um gráfico da corrente em um circuito em função do tempo. Como parte do teste, v