Um automóvel possui uma antena de rádio metálica de de comprimento, fixada na sua parte traseira. Considerando que, nessa região, o campo magnético da Terra é perpendicular à antena e vale , podemos afirmar que o valor máximo da fem induzida nessa antena quando o automóvel se desloca a uma velocidade de é:
Passo 1
Bora lá!! O que temos nessa questão? Bom, uma antena metálica, portanto, condutora, está na presença de um campo magnético , que é o mesmo em toda a região do espaço e não varia com o tempo (isso é importante e vamos discutir um pouco mais daqui a pouco…calma…). Essa espira se move com velocidade constante sempre perpendicular ao , blz?
Como a antena é metálica, os elétrons que constituem seu material estão em movimento e, por isso, sentem uma força ao se movimentarem. Essa movimento da barra, e portanto dos elétrons dela, faz com que apareça uma fem induzida, dada por:
sendo que está relacionado com o comprimento da antena. Até aqui tudo bem? A gente precisa encontrar para matar essa questão. Continua lendo com calma, vamos chegar lá…
Passo 2
A questão não dá uma figura, mas aqui com a gente não tem essa, a gente fez uma para acabar com essa questão de vez!! Como no enunciado, o campo é sempre perpendicular à barra metálica (Instigando você agora: mas não poderia ser um campo em , ou seja, ??).
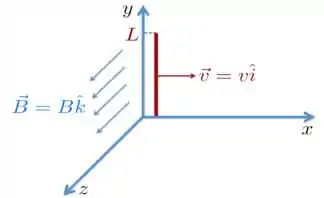
Então, o produto vetorial que aparece em fica:
O elemento de comprimento . Então é antiparalelo ao vetor (e se , como fica isso? Continua antiparalelo?). Como e são constantes, temos a seguinte integral:
Resposta
Substituindo os valores, temos
Portanto, letra a). \0/