Uma barra condutora de resistência desprezível, comprimento e massa , está deslizando para baixo em movimento uniforme com velocidade , sob ação apenas de sua força peso e de uma força magnética. Esta força é gerada pelo campo magnético externo (uniforme e constante) aplicado na direção entrando na folha de papel, e de módulo . A barra faz contato com trilhos condutores de resistência também desprezível e o circuito é fechado pela resistência .
Considere e que o campo magnético externo é muito intenso. De modo que o campo magnético devido à corrente induzida no circuito pode ser desprezado.
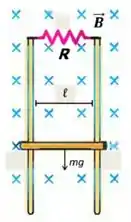
Responda, justificando, qual o sentido da corrente induzida no circuito (horário ou anti-horário) e qual o sentido do vetor força magnética sobre a barra (para cima ou para baixo).
Calcule o módulo da velocidade constante com que a barra desliza para baixo na montagem da figura.
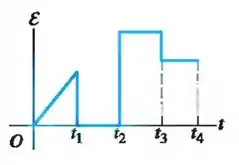
Agora a barra foi fixada numa certa posição. A induzida no circuito como função do tempo é dada no gráfico abaixo. Faça um esboço qualitativo do gráfico do módulo do campo magnético externo em função do tempo. Faça a suposição de que começa em zero e é contínuo durante todo o intervalo, explicitando no eixo os instantes , , e .
Passo 1
Podemos determinar o sentido da corrente através da Lei de Lenz! Como a área está aumentando, o fluxo magnético também está, logo, o campo induzido será contrário ao campo existente, fazendo a regra da mão direita, vemos que a corrente induzida flui no sentido anti-horário.
Para determinar a força magnética que atua na barra, basta usar a seguinte fórmula:
Como aponta da esquerda para a direita e está entrando no papel, a força estará apontando para cima!
Passo 2
Como a barra desce com velocidade constante, temos que a força magnética deve ser igual, em módulo à força peso, ou seja:
Sendo que . Logo:
Pela Lei de Faraday, temos:
Substituindo:
Passo 3
Para determinar com varia o campo magnético, precisamos lembrar da relação entre e o campo, pela Lei de Faraday, temos:
Logo, como a área é constante, a é proporcional à derivado do campo, logo o gráfico do campo deve parecer com algo assim:
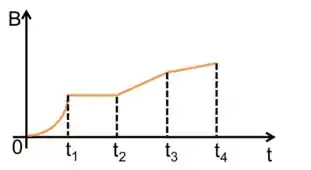
Resposta
Corrente no sentido anti-horário e Força apontando para cima.
Ver gráfico acima.