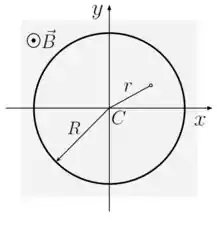
A figura mostra uma espira condutora circular de raio , localizada no plano . A espira está submetida a um campo magnético variável no tempo e no espaço dado por , onde e são constantes positivas e é a distância radial até o centro da espira. O campo magnético atua na região hachurada da figura, sendo perpendicular à página e apontando para fora da mesma. Nestas circunstâncias, determine:
(a) O fluxo magnético através da espira.
(b) A força eletromotriz induzida na espira.
(c) O sentido de circulação da corrente induzida (horário ou anti-horário) num instante de tempo finito . Justifique sua resposta.
Passo 1
Vamos resolver aqui os itens (a) e (b), beleza?
O primeiro passo é calcular o fluxo magnético através da espira. Para isso, vamos utilizar a própria definição de fluxo magnético, dada por:
O que precisamos analisar então para calcular a expressão acima? Vamos lá:
- O campo “sai” do papel, ou seja, aponta no sentido crescente da direção de ;
- O elemento de área , que é normal à superfície, também “sai” do papel;
- Isso significa que o produto escalar pode ser escrito como: .
Temos, então:
Passo 2
O próximo passo é substituir na expressão acima o valor do módulo do campo e do elemento .
Temos:
Passo 3
Para calcular a força eletromotriz induzida na espira, vamos utilizar a Lei de Faraday:
Resposta
(a) .
(b) .