Uma barra condutora de comprimento é apoiada sobre trilhos condutores fixos e indeformáveis, definindo um circuito retangular, mostrado na figura. A resistência equivalente do circuito é constante e vale . Parte da superfície deste circuito é penetrada perpendicularmente por um campo magnético constante e uniforme de módulo , entrando na página.
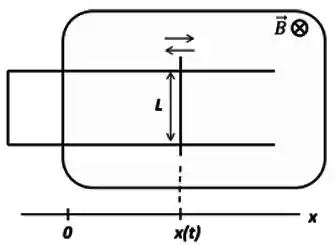
Por um mecanismo não mostrado na figura, a barra é forçada a oscilar, de modo que sua posição descreve um MHS (movimento harmônico simples), com equação dada por:
Calcule a fem induzida no circuito como uma função do tempo, .
Calcule o valor máximo da corrente induzida, .
Em uma nova situação, a barra é deixada em repouso na posição e o campo magnético, sem mudar sua orientação, varia no tempo de acordo com a função:
Encontre o valor máximo da corrente induzida.
Passo 1
Para determinar a fem induzida, vamos utilizar a Lei de Faraday, ela dos diz:
Vamos primeiro calcular o fluxo , se liga!
Arbitrando o vetor área no mesmo sentido do campo magnético, temos:
Sendo a área , substituindo o fluxo na equação da Lei de Faraday, temos:
Sabemos como varia em função de , pela equação que foi dada no enunciado:
Calculando a derivada, temos:
Substituindo na Lei de Faraday:
Vamos agora substituir os valores do campo e do comprimento da barra!
De onde surgiu aquele na fórmula acima?
Bom, o campo é dado em Tesla, ou seja, , no entanto, estamos utilizando a unidade centímetros e não metros. Por isso devemos dividir por , para que a unidade do campo vire ! Show??
Passo 2
Vamos determinar a corrente em função do tempo. Temos a nossa velha e conhecida fórmula:
Substituindo a função da fem, temos;
A corrente máxima ocorre quando , portanto:
Passo 3
Para resolver esse item, vamos fazer o mesmo mimimi que fizemos no item só que agora, temos como valor fixo e quem varia é o campo .
Vamos começar com a Lei de Faraday:
Vamos primeiro calcular o fluxo , se liga!
Arbitrando o vetor área no mesmo sentido do campo magnético, temos:
Sendo a área , substituindo o fluxo na equação da Lei de Faraday, temos:
Vamos agora calcular a derivada do campo magnético, se liga:
Substituindo na equação da tensão, e substituindo os valores de e , temos:
Veja que dessa vez estamos passando tudo para metro, pois o campo está em Tesla !
A corrente é dada por:
A corrente máxima ocorre quando , ou seja:
Resposta
.
.
.