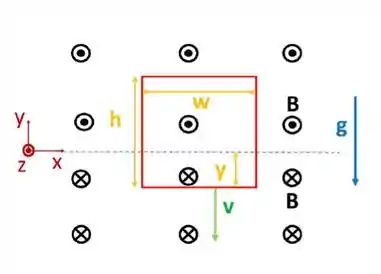
Um arame metálico forma um circuito retangular, de altura , largura e massa. Esse arame tem uma resistência total igual a . Na Figura, podemos ver que, em um certo instante de tempo, uma parte do aro está e outra em . O plano (linha azul tracejada) separa a região onde o campo magnético aponta na direção da região onde o campo magnético aponta na direção , como mostra a Figura. Observe a distância entre a linha tracejada azul e o braço horizontal inferior da espira.
Se , temos ; Se , .
Suponha que esse aro cai com velocidade vertical v constante sob a ação apenas de seu próprio peso e das forças magnéticas agindo sobre ele. Todas as respostas abaixo devem ser apresentadas apenas em função das variáveis do problema: (use apenas as necessárias).
Quando o aro está colocado como mostra a Figura, para todos os itens:
- Calcule a taxa de variação no tempo do fluxo magnético sobre o aro
- Calcule a sobre o aro e a corrente induzida. Seu sentido é horário ou anti horário? Justifique sua resposta
- Calcule a força magnética resultante sobre o aro
- Calcule o valor da velocidade constante com que o aro cai. Lembre-se que a velocidade é um vetor
- Calcule o valor da potencia elétrica dissipada no aro
- Calcule a potencia fornecida elo trabalho da força peso sobre o aro. Calcule
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
Vamos começar pelo vetor normal à superfície: . Para o fluxo, teremos duas contribuições, da área da parte inferior da espira e da área da parte superior. Daí o fluxo magnético fica:
E a variação temporal do fluxo é a derivada no tempo dessa expressão:
E sabemos que é igual a velocidade :
Passo 2
Letra (b):
A pode ser obtida através da lei de Lentz! Saca só:
E a corrente induzida pode ser encontrada através da lei de ohm:
E o sentido? O sentido é o anti-horário, pois e cria um fluxo positivo, se opondo à mudança.
Passo 3
Letra (c): agora vamos calcular a força.
A força total vai ser a soma de cada uma das forças em cada fio. Em um deles, a força vai ser:
O vetor deslocamento tem módulo e na direção perpendicular de cada um dos campos . O ângulo entre eles é , assim a força em um deles é:
E a força total é o dobro desse valor:
Show! Vamos pra letra (d)?
Passo 4
Letra (d):
A resultante total sobre o aro é nula, pois a velocidade é constante e isso significa que a aceleração e a força resultante são iguais a zero.
Sendo assim, só temos a força gravitacional (apontando para baixo) e a força magnética (apontando para cima):
E daqui podemos achar o valor da velocidade :
Tranquilo? Então borá pra letra (e)!
Passo 5
Letra (e):
A potência elétrica dissipada é dada por:
A corrente já foi calculada, então agora é só substituir:
E agora usando a expressão para a velocidade que encontramos no passe anterior temos:
Beleza até aqui? Vamos para o último item?
Passo 6
Letra (f):
E a potência é dada através da velocidade:
Usando a expressão para a velocidade do item (d) temos:
E essa é exatamente a expressão para a encontrada no passo anterior! Assim a razão entre as potências fica:
Beleza?
Pronto pra próxima questão? =)