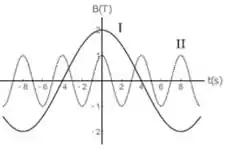
. Considere duas situações: na primeira, uma espira circular de área é atravessada perpendicularmente por um campo magnético uniforme que oscila periodicamente no tempo de acordo com a curva na figura abaixo (curva cheia), e na segunda situação a mesma espira é atravessada perpendicularmente por um campo magnético uniforme oscilante descrito pela curva (curva pontilhada). Podemos afirmar que a menor amplitude do fluxo de campo magnético e a maior amplitude da força eletromotriz induzida ocorrem, respectivamente, nas situações:
Escolha uma:
e
. e
. Não é possível determinar sem conhecer a resistência elétrica da espira
. e
. e
Passo 1
Vem comigo que a gente detona essa questão juntos!
Primeiro precisamos saber como é a cara desses campos magnéticos, olhando o gráfico a gente pode ver que eles têm um comportamento da seguinte forma:
Onde é amplitude do campo e , onde é o período de oscilação do campo e é a fase do campo.
Podemos tomar para os dois campos, já que em eles têm o valor máximo, então podemos escrever a expressão de cada campo, da seguinte forma:
Passo 2
Olhando o gráfico a gente pode ver que em corresponde a do período de e a período de , assim:
Com isso podemos tirar a seguinte relação:
E sabendo que:
Temos que:
Passo 3
Vamos então analisar o fluxo magnético de cada campo. Como esse campo é uniforme e é perpendicular a área da espira, esse fluxo é dado por:
Então:
Nós já sabemos que a amplitude de é maior que de , então temos que:
Passo 4
A força eletromotriz é dada por:
Então temos que:
A amplitude de é maior que , então temos que:
Então a única alternativa correta é a letra .
Resposta
e