Uma espira retangular, de comprimento , largura e resistência , é colocada na vizinhança de um fio infinitamente longo que transporta uma corrente .
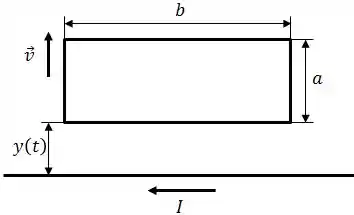
Suponha que a espira está se afastando do fio com uma velocidade constante . Considere que a distância inicial entre a espira e o fio vale .
Calcule o fluxo do campo magnético produzido pelo fio longo na espira em função da posição lateral .
Calcule a induzida e a corrente induzida na espira.
Considere agora o caso em que a corrente no fio infinito pode variar com o tempo. Para que a induzida na espira seja nula, essa corrente deve aumentar, diminuir ou se manter constante? Justifique.
Passo 1
Calcule o fluxo do campo magnético produzido pelo fio longo na espira em função da posição lateral .
O fluxo magnético, por definição, é dado por:
O campo magnético aqui é o gerado pelo fio que transporta a corrente e é dado por:
Onde é a distância entre o fio e o ponto onde estamos calculando o campo magnético.
Utilizando a regra da mão direita, onde o polegar representa a corrente elétrica, vemos que, na região da espira o campo magnético aponta para o dentro do plano da página, perpendicular ao mesmo.
Além disso, como o campo magnético varia com , podemos escrever a porção infinitesimal da área como:
Como mostra a figura abaixo:
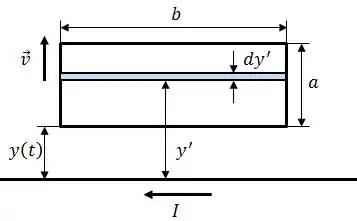
Legal! Agora vamos calcular o fluxo magnético:
Passo 2
Calcule a induzida e a corrente induzida na espira.
A induzida é obtida através da Lei de Faraday, dada por:
Para calcular a derivada, vamos usar a seguinte expressão do fluxo magnético:
Assim, teremos:
Da expressão do fluxo magnético somente varia com o tempo, então podemos tirar o resto da derivada, beleza?
Dessa forma, teremos:
Onde .
Só pra deixar mais arrumadinho:
Passo 3
Beleza, agora falta calcular a corrente induzida.
Uma vez que já calculamos a induzida, a corrente no circuito vai ser dada por:
Logo:
Passo 4
Considere agora o caso em que a corrente no fio infinito pode variar com o tempo. Para que a induzida na espira seja nula, essa corrente deve aumentar, diminuir ou se manter constante? Justifique.
Vamos voltar para a expressão da Lei de Faraday, beleza?
Para que a induzida seja nula, é necessário que o fluxo magnético seja constante através da espira.
Conforme o valor de aumenta, o logaritmo diminui. Dessa forma, para que o fluxo permaneça constante, a corrente deve aumentar com o tempo.
Resposta
A corrente deve aumentar com o tempo.