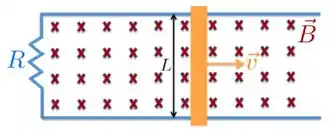
Um circuito fechado é formado por uma barra metálica de comprimento , que desliza com velocidade sobre um suporte metálico fixo, com uma resistência , imerso em um campo magnético uniforme e estacionário , perpendicular ao plano do circuito.
3a) A corrente induzida no circuito vale:
- 0,1 A
- 0,2 A
- 0,3 A
- 0,4 A
- 0,5 A
3b) A potência total entregue pelo agente externo para mover a barra:
- 0,5 W
- 2,0 W
- 2,5 W
- 3,0 W
- 5,0 W
Passo 1
Primeiro passo fundamental, galera, é tentar pegar os aspectos importantes do enunciado. Bom, vamos lá!!
Temos uma barra condutora que desliza sobre um suporte fixo. A barra e esse suporte definem uma área, correto? Essa área está aumentando com o tempo, pois o comprimento mostrado na figura abaixo está aumentado à medida que a barra desliza para a direita, enquanto o comprimento permanece o mesmo. Ok?
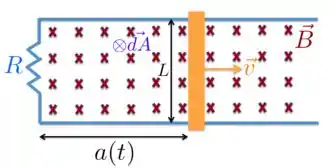
Por outro lado, como área aumenta com o tempo, mais linhas de campo entram no plano dessa área (para dentro do plano da página!) à medida que a barra se desloca com velocidade para a direita. Isso significa, que o fluxo magnético através dessa área está variando com o tempo.
Portanto, aparece uma fem induzida e, como a barra e suporte são feitos de material condutor, há também uma corrente induzida que circula no sistema.
Passo 2
Agora, como a gente já sabe que tem fluxo magnético variável com o tempo e, por isso, tem uma fem induzida, vamos calcular explicitamente o valor de .
Para isso, dá uma olhada na figura acima e veja que coloquei o elemento de área entrando no plano e paralelo ao campo magnético . Com isso, o fluxo magnético é dado por
Aqui entra uma informação fundamental do problema: é uniforme. Isso significa, pessoal, que o campo magnético é o mesmo em todos os pontos da região da área da figura. Bom, em termos de conta, isso é equivalente a retirar da integral acima!!
Com isso, é simplificado para
o que mostra, claramente, que o fluxo magnético varia no tempo porque o comprimento varia com o tempo!!
Passo 3
Para calcular a fem e a corrente induzida, precisamos da informação de que o campo magnético, além de ser uniforme (o mesmo em todos os pontos do espaço!) como discutimos, deve ser, também, estacionário. Esta informação nos diz que não varia no tempo! Por quê isso é importante??
Como o módulo a fem induzida é proporcional à taxa de variação temporal de , vamos apenas derivar o comprimento ! Portanto, temos o seguinte:
Como , que é o módulo da velocidade da barra, a fem induzida é
Substituindo os valores do enunciado, chegamos a
Passo 4
Para o cálculo da potência, precisamos da seguinte expressão
Resposta
Portanto, as respostas são as seguintes:
3a) letra e)
3b) letra c)