UFRJ – Física 3 – 2020.2 – PF – M.Escolha
. Uma espira retangular, rígida, de lados e , condutora, executa um movimento oscilatório ao longo da direção do eixo , de modo que a coordenada do seu centro é dada por:
onde é uma constante positiva e é um instante genérico. Além disso, temos um campo magnético constante de módulo que aponta para fora do plano da página, conforme mostra a figura abaixo .
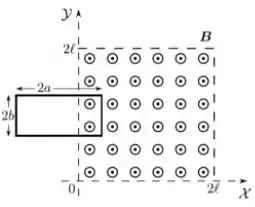
Considerando que o vetor normal ao plano da espira aponta no mesmo sentido do campo, definindo a orientação na qual a força eletromotriz induzida é positiva, em qual instante abaixo a força eletromotriz induzida na espira é máxima?
Escolha uma opção:
Passo 1
Vem comigo que essa questão não tem vez!
A força eletromotriz pode ser dada por:
Então ela é igual a menos a variação do fluxo do campo magnético. Esse fluxo é dado pelo campo magnético vezes a área por onde esse campo passa. No caso do nosso problema essa área é dada por:
Onde nos dá a parcelada do comprimento da espira que está dentro do campo.
Passo 2
Juntando tudo o nosso fluxo é dado por:
Derivando isso no tempo, temos:
Então temos que:
Para que esse cara seja máximo temos que:
Logo:
Então nossa alternativa é a letra .