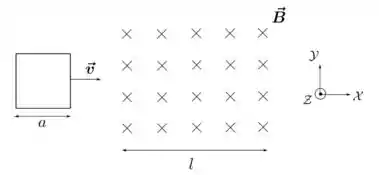
Uma espira condutora quadrada de lado e resistência elétrica desloca-se em movimento retilíneo uniforme com velocidade (), de forma que dois de seus lados permanecem paralelos ao eixo , como mostrado na figura abaixo. Ela atravessa uma região de campo magnético uniforme e estacionário , que se estende ao longo de uma região de comprimento ao longo do eixo e por todo o eixo . Para os cálculos abaixo, escolha o vetor unitário (ou versor) normal à área definida pela espira como , ou seja, entrando no plano da folha.
- Determine a intensidade e o sentido da corrente induzida na espira em três situações: quando ela está entrando na região do campo, quando está totalmente imersa nessa região e quando está saindo dessa região.
- Determine a força magnética sobre a espira (módulo, direção e sentido) nas mesmas três situações do item anterior.
- Faça gráficos separados da intensidade do fluxo de campo magnético sobre a espira e da corrente na espira como função do tempo . Considere o instante em que a espira começa a entrar na região do campo e destaque os intervalos de tempo correspondentes às três situações acima. Atribua sinais positivo e negativo para o sentido corrente de acordo com a orientação do vetor normal mencionado acima.
Passo 1
Na figura abaixo são representadas cada uma das situações mencionados no enunciado. A área, como pedido na questão, é orientada paralelamente ao vetor e, portanto, assim como este, também está entrando no plano da página. Por isso, o sentido positivo para a fem e a corrente induzidas é horário, como indicado pelo sinal na figura abaixo.
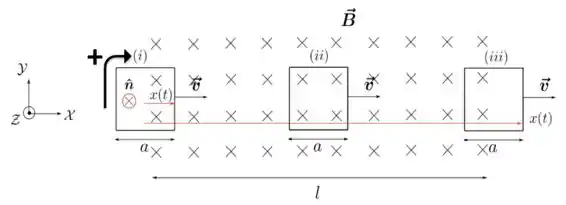
Antes de começar a analisar cada situação separadamente, note que o fluxo de campo magnético é sempre positivo, pois é sempre paralelo à área atravessada pelas linhas de campo em cada um dos instantes de seu movimento.
Na situação , a espira quadrada está entrando na região onde há campo. Então, à medida que ela entra nessa região, mais linhas de campo atravessam sua área, correto?
Aqui começo te perguntando: se o campo é uniforme (o mesmo em todos os pontos da região!) e estacionário (não varia com o tempo!) e a área da espira também não muda, o que poderia variar nesse caso?
Bom, a área da espira por onde as linhas de campo passam aumenta à medida que a espira com velocidade constante entra na região e essa é a razão pela qual esperamos encontrar em uma corrente induzida! Agora, qual o sentido dela?
Ao se deslocar para dentro do campo, o fluxo magnético, que é sempre positivo, (pois é sempre paralelo à área da espira!), aumenta, pois mais linhas de campo atravessam sua área. Isso significa que a taxa de variação do fluxo é positiva:
isto é, o fluxo está aumentando com o tempo e aparecem uma fem e uma corrente induzidas, ambas negativas, na espira no sentido anti-horário.
Agora para um pouco, respira e verifica se essa discussão ficou clara para vocês....Tenta acompanhar a solução sempre olhando para a parte da figura correspondente.
Respirou? Conferiu se a ideia da situação ficou clara? Se sim, pode seguir agora...
Na situação , como o campo é uniforme e estacionário e a quantidade de linhas de campo que atravessam a área da espira é sempre a mesma, o fluxo magnético nesse caso é constante: . Por isso, temos o seguinte
e, como não fem induzida, também não há corrente induzida neste caso.
Na situação ocorre exatamente o oposto da situação , pois, agora, a área que é atravessada pelas linhas de campo está diminuindo com o tempo. Por isso, o fluxo magnético, apesar de positivo, , tem sua taxa diminuindo com o tempo, ou seja,
Assim, como a fem induzida é positiva, a corrente induzida também tem sentido positivo, o que significa que está circulando no sentido horário.
Passo 2
Agora que já sabemos quais os sentidos das correntes induzidas em cada uma das situações, vamos encontrar a intensidade de cada uma delas. Para isso, precisamos calcular a fem induzida para cada caso.
Como campo magnético é uniforme (o mesmo em todos os pontos!) e estacionário (não varia com o tempo!), em toda a superfície da espira condutora ele tem o mesmo valor. Por isso, o campo pode sair da integral do fluxo magnético e obtemos o seguinte
onde , sempre paralela a , é a área atravessada pelas linhas de campo.
Essa expressão para vale para cada uma das situações que estamos discutindo nesta questão. Por isso, sugiro que confirme se o desenvolvimento dessa expressão está OK para você...
Se está tudo tranquilo até aqui, continuemos! Respira fundo e....bora lá
Na situação , , pois essa é a área pela qual passam as linhas de campo nesse caso. Por isso, o módulo da fem induzida é
Como a fem induzida é dada por , temos que
Na situação , como a área atravessada pelo campo diminui com a mesma taxa que aquela da situação , a corrente induzida tem o mesmo módulo, isto é,
Os Passos 1 e 2 são referentes ao item a) da questão!!
Passo 3
Considerando o item b) da questão, para calcularmos a força magnética resultante, usaremos a expressão
em que é o vetor cuja direção e sentido é dado pelo sentido em que a corrente circula na espira.
Na situação , como a corrente induzida está no sentido anti-horário, o vetor em cada lado da espira é representado na figura abaixo pelas setas azuis. Realizando o produto vetorial de com o campo nos lados da espiras que são paralelos ao eixo , vemos que as forças nesses segmentos são de mesmo módulo, mesma direção, porém sentidos contrários: e . Portanto, a força resultante na direção é zero!
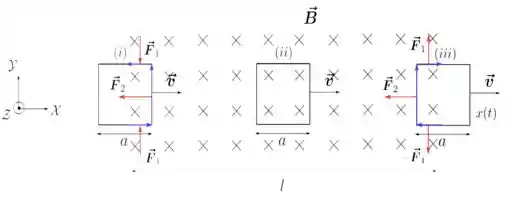
Com isso, só precisamos calcular a força que atua no lado da espira paralelo ao eixo , como indicado na figura acima.
Nesse caso, temos os seguintes vetores: e . Portanto, como , temos
Como .
Na situação , como vimos, . Isso significa que a força resultante na espira nesse caso é zero.
Na situação , a corrente induzida está no sentido horário e, por isso, o produto ainda produz uma força na lateral paralela ao eixo no mesmo sentido que no caso , ou seja, uma força também apontando para o sentido . O módulo dessa força é igual ao caso e, por isso, temos uma força também dada por
Repare que nos lados da espira paralelos ao eixo , as forças continuam se cancelando e não contribuem para a força resultante.
Passo 4
Discutindo o item c):
Antes de esboçarmos os gráficos, vamos estudar um pouco sobre os intervalos de tempo relacionados ao movimento da espira. No tempo , a espira começa a entrar na região de campo. Vamos separar essa discussão sobre o intervalo tempo em três etapas:
1) Como o movimento é MRU ( é constante), aumenta linearmente com o tempo e ela gasta um tempo para entrar totalmente na região de . Ela também leva um tempo igual a para poder sair dessa região.
2) Agora, considere o lado vertical da espira mais à sua esquerda, que a gente destaca lá na figura usando a chave em preto. Depois que a espira entrou totalmente dentro da região de campo, esse lado vertical gasta um tempo para chegar até o final da região de campo magnético.
Concorda? Checa isso lá na figura para não restarem dúvidas..
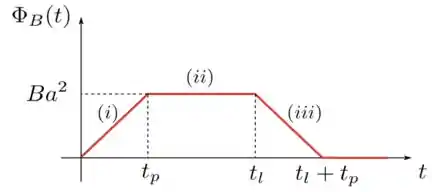
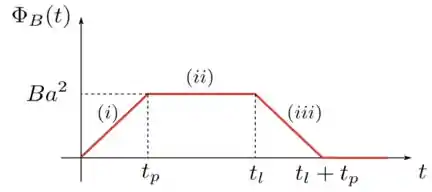
Uma vez que já estudamos sobre os intervalos de tempo, vamos resumir o que descobrimos sobre o fluxo magnético e sua taxa de variação com o tempo e colocar tudo junto num gráfico:
- Na situação , o fluxo magnético, que é sempre positivo (), aumenta com o tempo à medida que a espira vai entrando na região de campo magnético e tem valor máximo quando a espira está toda dentro do campo. Como a velocidade da espira é constante, a área atravessada pelo vai aumentando linearmente com o tempo e, por essa razão, durante o tempo o .
- Na situação não há corrente induzida, pois o fluxo magnético é sempre constante e igual a em todo o percurso da espira. Existe fluxo magnético, mas ele permanece o mesmo durante todo o tempo que a espira fica totalmente dentro da região de campo.
- Na situação , a espira começa a sair da região de campo e a área atravessada pelas linhas de diminui com o tempo. O fluxo magnético é positivo, como em todos os casos deste problema, porém, à medida que o tempo passa, seu valor diminui até se anular completamente, que é quando a espira está toda fora da região de campo. Por isso, do tempo até o instante , .
Se juntamos essas informações sobre o intervalo de tempo e sobre o fluxo magnético na espira, construímos o seguinte gráfico.
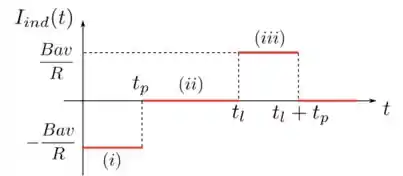
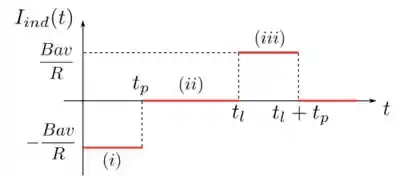
Para plotarmos a corrente induzida em função do tempo, precisamos nos lembrar que
- Na situação , a corrente induzida é negativa e tem módulo durante o intervalo de tempo .
- Na situação , a corrente induzida é nula no intervalo de tempo .
- Na situação , a corrente induzido é positiva e tem módulo .
- Depois que a espira sai totalmente do campo, não há mais fluxo magnético, por isso a corrente induzida depois de um tempo é nula.
Resposta
a)
Na situação
Sentido: Anti-horário
Na situação
Na situação
Sentido: Horário
b)
Na situação
Na situação
Na situação
c)