Na figura abaixo dois trilho condutores retilíneos formam um ângulo reto. Uma barra condutora em contato com os trilhos parte do vértice no instante , com uma velocidade constante .
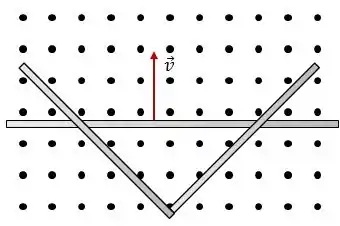
Há um campo magnético dirigido para fora da página, em toda a região. Determine:
- O fluxo magnético em função do tempo ;
- A induzida aplicada ao triângulo em função do tempo;
- Se a , onde e são constantes, e sabendo o valor de para , determine o valor de .
Passo 1
a) O fluxo magnético em função do tempo ;
Por definição, o fluxo magnético é dado por:
Como o campo magnético é constante:
Onde é a área do triângulo.
A área de um triângulo é dada por:
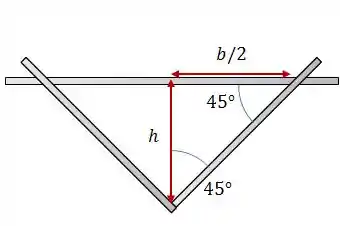
Analisando a geometria do problema, podemos ver que . Logo:
Como a barra horizontal se desloca com velocidade constante , podemos relacionar a velocidade com a altura da barra por:
Portanto, o fluxo magnético será dado por:
Passo 2
b) A induzida aplicada ao triângulo em função do tempo;
De acordo com a lei de Faraday, a induzida é dada por:
Agora ficou fácil, é só derivar o cara que achamos no passo 1.
Passo 3
c) Se a , onde e são constantes, e sabendo o valor de para , determine o valor de .
Eu sei que essa agora pode parecer viagem, mas o negócio aqui é só comparar com a expressão da que já tínhamos encontrado.
Para que os dois lados sejam iguais:
Acabou!
Resposta
a.
b.
c.