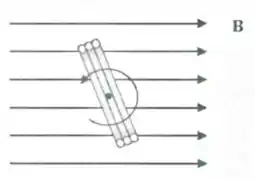
Uma bobina condutora consistindo de voltas de fio gira em torno de um eixo, paralelo ao plano da bobina e passando por seu centro, como mostra a figura. A bobina tem área e gira com uma velocidade angular constante em uma região onde há campo magnético uniforme e constante, que induz uma (variável no tempo) na bobina. Qual é a magnitude desta com função do tempo?
Passo 1
Para entendermos bem o que está acontecendo aqui, precisamos nos lembrar de como é o fluxo magnético . A expressão dele é:
sendo o ângulo entre os vetores campo magnético e o elemento de área orientado . Esse vetor área é sempre orientado perpendicular à área que, no nosso caso aqui, fica como está desenhado na figura abaixo.
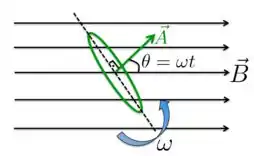
Mas como as espiras giram em torno do eixo com velocidade angular constante , isso significa que o ângulo entre e é: .
Agora, antes de a gente seguir para as contas, vamos pensar um pouco no que está rolando aqui. As áreas das espiras não estão variando no tempo. Como o problema disse que o campo é constante, também não varia no tempo, além de ter o mesmo valor em todos os pontos do espaço, já que é uniforme.
O que está mudando com o tempo então? O ângulo entre os vetores e !! Por isso, temos um fluxo magnético variável no tempo e isso fará com que apareça uma fem induzida nas espiras.
Passo 2
Como o campo magnético é uniforme, ou seja, tem o mesmo valor em todos os pontos, e , podemos simplificar a expressão para fluxo magnético através das espiras:
Como o campo magnético é constante, assim como as áreas das espiras, a fem induzida será dada por:
Simplificando essa expressão:
Resposta
Letra a.