Uma barra condutora de comprimento e resistência desprezível desliza sem atrito sobre dois trilhos condutores, como mostra a figura.
Dois resistores e são ligados às extremidades dos trilhos, fechando os dois circuitos. Um campo magnético uniforme está dirigido perpendicularmente para “dentro” da página. Um agente externo puxa a barra para a esquerda com velocidade constante.
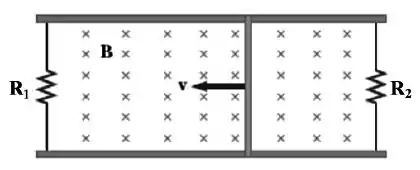
Encontre:
A potência total dissipada no circuito;
O valor e o sentido das correntes em ambos os resistores;
O vetor força magnética que age sobre a barra;
Passo 1
A potência total dissipada no circuito;
Bom, tem algumas fórmulas conhecidas para a potência:
Como temos dois resistores, a potência total será a soma das potências dissipadas nos dois resistores.
Assim, vamos calcular a pela Lei de Faraday nos dois resistores, calcular as suas potências e soma-las no final das contas. Beleza?
Partiu!
Pela Lei de Faraday:
Como, em ambas as malhas, o campo magnético é constante:
A única diferença entre as duas malhas é que em uma o fluxo magnético está aumentando e, na outra, o fluxo magnético está diminuindo.
Portanto, a potência total dissipada será:
Passo 2
O valor e o sentido das correntes em ambos os resistores;
Já calculamos a nos dois resistores certo?
Então basta usar a Lei de Ohm para calcular as correntes em cada resistor. Como estamos preocupados com o valor, não vamos nos preocupar com esse sinal negativo.
Logo:
Para calcular o sentidos das correntes, teremos que recorrer à Lei de Lenz.
De acordo com a Lei de Lenz:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Simplificando... a corrente induzida é sempre do contra, se o fluxo magnético através da espira estiver aumentando, a corrente induzida vai gerar um campo magnético no sentido contrário, só pra atrapalhar... se o fluxo magnético estiver diminuindo, a corrente induzida vai gerar um campo magnético a favor.
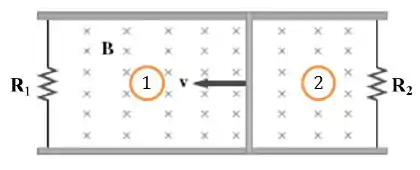
- Malha 1
- Malha 2
Na malha 1, conforme a barra se movimenta, a área diminui. Portanto, o fluxo magnético está diminuindo na malha 1. Assim, a corrente induzida vai gerar um campo induzido no mesmo sentido do campo magnético . Como o campo magnético na malha 1 tem sentido entrando na página... o campo magnético induzido também vai ter sentido entrando na página.
Pela regra da mão direita, para que o campo magnético gerado pela corrente induzida esteja entrando na página, a corrente induzida que passa pelo resistor 1 deve estar no sentido horário.
Na malha 2, conforme a barra se movimenta, a área aumenta. Portanto, o fluxo magnético está aumentando na malha 2. Assim, a corrente induzida vai gerar um campo induzido que se oponha a esse aumento. Como o campo magnético na malha 2 tem sentido entrando na página... o campo magnético induzido vai ter sentido saindo da página.
Pela regra da mão direita, para que o campo magnético gerado pela corrente induzida esteja saindo da página, a corrente induzida que passa pelo resistor 2 deve estar no sentido anti-horário.
Passo 3
O vetor força magnética que age sobre a barra;
A força magnética sobre um condutor retilíneo carregado é dado por:
Onde está no mesmo sentido da corrente que passa pelo condutor.
A corrente na malha 1 está no sentido horário e a corrente na malha 2 está no sentido anti-horário, como vimos na letra .
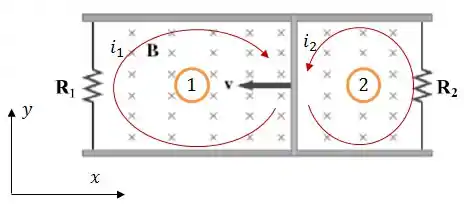
Assim, na barra, as duas correntes se somam e se deslocam no sentido .
Assim, a força magnética na barra será:
Resposta
A corrente induzida que passa pelo resistor 1 deve estar no sentido horário.
A corrente induzida que passa pelo resistor 2 deve estar no sentido anti-horário.