Uma espira retangular muito longa, de largura , resistência e massa , está inicialmente suspensa na presença de um campo magnético horizontal uniforme orientado para dentro do papel, que existe apenas acima do segmento de reta . Deixa-se cair a espira, que acelera sob ação da gravidade até atingir uma velocidade terminal .
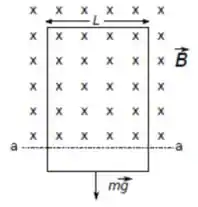
a) Calcule a força eletromotriz induzida na espira, em função dos dados acima e da sua velocidade.
b) Calcule a intensidade e determine o sentido da corrente induzida (explique a sua resposta) na espira, em função dos dados acima e da sua velocidade.
c) Obtenha uma expressão para ignorando a resistência do ar.
Passo 1
Nesse problema vamos a lei da indução de Faraday:
Com isso, se o fluxo magnético na espira variar com o tempo, uma corrente induzida vai aparecer na espira.
Para resolver esse tipo de problema, ajuda muito estabelecer um sistema de coordenadas:
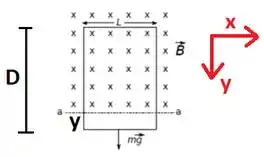
Colocando o eixo para direita e o eixo para baixo, o eixo apontará para dentro da tela, mesma direção do campo magnético. O fluxo magnético é definido por
Como o campo é uniforme, essa relação pode ser escrita como
Vamos adotar o vetor normal . Assim, , de modo que
Como adotamos a normal para dentro da tela, a orientação positiva da corrente induzida na espira é o sentido horário (regra da mão direita).
Passo 2
Como , e são constantes, temos que
Mas é a velocidade com que a espira cai, de modo que
Portanto,
Essa é a fem induzida na espira devido à variação do fluxo magnético!
Passo 3
No item (b), nós queremos achar a corrente induzida no circuito. Para isso, usamos
Usando a resposta do item (a):
Como essa corrente é positiva, pela orientação que escolhemos ela circula a espira no sentido horário.
Passo 4
O item (c) é o mais complicadinho. Queremos saber qual é a velocidade terminal de queda da espira. Como diabos fazer isso?
Primeiro vamos olhar para a corrente calculada no item anterior percorrendo a espira:
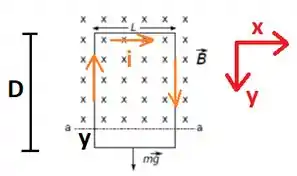
Quando um fio em que passa correte está sob ação de campo magnético aparece uma força magnética no fio:
No caso da espira, a parte dela que está na região onde existe o campo deve sofrer essa força. As forças nos fios laterais vão se cancelar, de modo que só importa o fio de cima. Nele, e . Portanto,
Desta forma, enquanto a gravidade puxa a espira na direção , a força magnética é oposta. Podemos escrever a segunda lei de Newton para essa situação:
Usando e , temos que
Daqui nós poderíamos resolver a equação diferencial e achar . Mas não é isso que o problema pergunta. Ele quer saber a velocidade terminal.
Passo 5
Como a força de resistência é proporcional a velocidade, vai chegar um momento que a velocidade da espira vai ser tal que a força de resistência do ar vai anular o peso e a força resultante passará a ser zero. Nessa situação, o corpo cai com velocidade constante e essa velocidade é a velocidade terminal.
Para achar essa velocidade, basta fazer :
Assim,
Com isso terminamos o problema 😉.