Unicamp - Física 3 – P3 2018.1 - NOTURNO - 3
Uma espira quadrada condutora de lado é puxada, com aceleração constante, de uma região onde não existe magnético algum para outra região onde existe um campo magnético uniforme e estacionário perpendicular ao plano da espira. Durante o processo, a corrente induzida na espira:
- Será nula;
- Aumentará linearmente com o tempo;
- Será de algum valor constante diferente de zero;
- Aumentará exponencialmente com o tempo;
- Aumentará linearmente com o quadrado do tempo;
Passo 1
Para matarmos esta questão, dá uma olhada na figura abaixo, em que a gente colocou a espira quadrada de lado no momento em que ela está entrando na região onde tem campo magnético.
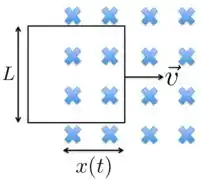
No momento em que a espira começa a entrar nessa região, existe uma área que varia no tempo. Por isso, o fluxo magnético também vai variar com o tempo e aparecerá uma corrente induzida.
Como o campo magnético é uniforme (tem o mesmo valor em todos os pontos da região), o fluxo magnético será dado apenas por
Portanto, o módulo da fem induzida será
em que é a velocidade da espira.
Passo 2
Como a aceleração da espira é constante, isso significa que a velocidade varia linearmente com o tempo
sendo a velocidade inicial. Se a espira tem resistência , então,
o que mostra que a corrente induzida aumentará linearmente com o tempo.
Resposta
Letra b.