Uma espira quadrada de lado é percorrida por uma corrente no sentido anti-horário. A corrente varia com o tempo e é dada por , onde é uma constante.
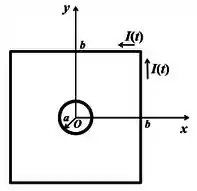
(a) Usando a lei de Biot-Savart, calcule o vetor campo magnético produzido pela espira quadrada na origem do sistema de coordenadas.
(b) Considere um anel condutor de raio centrado na origem. Calcule a corrente induzida no anel pela espira quadrada e indique seu sentido. Considere que o anel possui resistência . Sugestão: Assuma que o campo magnético produzido pela espira quadrada é uniforme próximo à origem do sistema de coordenadas.
Passo 1
A lei de Biot-Savart nos diz que:
Vamos começar calculando para um dos lados (o da direita):
onde é o ângulo entre e e . Temos que:
Fazemos . Temos:
Por fim, como ,
Por simetria, o campo magnético produzido pelos quatro lados da espira é obtido como:
Passo 2
Para o item (b), determinamos inicialmente a força eletromotriz através da lei de Faraday:
A corrente induzida (em módulo) será dada por:
Para determinar seu sentido, pensamos na Lei de Lenz: o campo está aumentando no sentido positivo do eixo e, portanto, o fluxo também estará. Assim sendo, a corrente induzida se opõe a esse crescimento, gerando uma corrente no sentido horário.
Resposta
(a)
(b) no sentido horário.