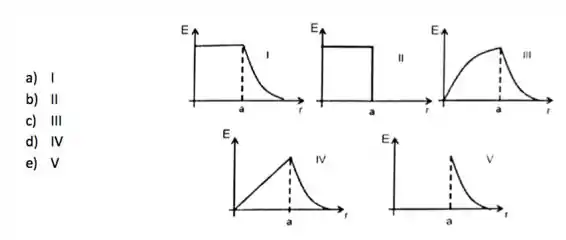
Um campo magnético uniforme passo pelo interior de uma região circular de raio e é perpendicular ao plano definido por essa região e sua intensidade aumenta a uma taxa constante . O gráfico que melhor representa o módulo do campo elétrico induzido para pontos internos e externos à região onde é diferente de zero vale:
Passo 1
Para facilitar a resolução e o entendimento desta questão, neste Passo 1, vamos apenas ilustrar e discutir a situação do enunciado através da figura abaixo. Essa representação vai nos ajudar bastante a resolver esse problema e outros similares. Vamos lá! Tenta acompanhar a discussão abaixo lentamente, lendo com cuidado, porque essa questão é típica das provas...
Vamos tomar uma região de raio que delimita uma área com um contorno orientado cujo elemento é tangente a cada ponto dessa curva. Perpendicular a essa região, há um campo magnético que varia com o tempo e sua intensidade aumenta com uma taxa constante , como mostra a figura abaixo.
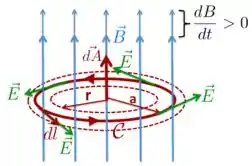
Além disso, colocamos o elemento de área paralelo à e, durante todo o tempo em que o campo aumenta, esses dois vetores são paralelos. Faremos a análise para os casos em que e utilizando, para isso, as curvas tracejadas da figura acima.
Você deve estar se perguntando sobre o vetor que aparece lá na figura...Em nossa discussão sobre a física dessa questão, você vai ver como ele aparece... :-0
Passo 2
Temos uma situação em que o campo magnético é sempre perpendicular à uma região de raio , mas sua intensidade aumenta de maneira constante com o tempo. Portanto, existe um fluxo magnético variável com o tempo através da área que o contorno delimita. Essa variação do fluxo magnético produz uma fem induzida no contorno .
Matematicamente, a gente pode escrever a fem induzida como
em que é campo elétrico, de origem não eletrostática, que aparece lá na figura. Agora, por que esse campo é sempre tangente ao contorno ? Vamos ver isso com cuidado!!
Se o campo elétrico tivesse alguma componente radial, ou seja, alguma componente ao longo da direção do raio , isso indicaria a presença de carga dentro da região , pois poderíamos pensar em superfície gaussiana cilíndrica envolvendo toda a região de raio e o fluxo através dessa gaussiana seria diferente de zero pela lei de Gauss! Concorda?
Por isso, como nessa questão não há carga dentro da região do contorno , então o campo elétrico é sempre tangente a todos os pontos de e tem o mesmo valor em todos esses pontos. Assim, como é sempre paralelo ao elemento , podemos escrever que
sendo o comprimento do circuito . Vamos olhar agora como fica o termo .
Passo 3
Vamos nos concentrar no fluxo magnético . é sempre paralelo à área da região de raio . Se consideramos um instante de tempo arbitrário, o campo que atravessa a área tem o mesmo valor em todos os seus pontos. Isso nos permite representar o fluxo magnético através de uma área de raio como
sendo que podemos considerar regiões em que e . Essa expressão nos mostra que o fluxo magnético varia porque o campo magnético aumenta com o tempo a uma taxa constante .
Passo 4
Agora, vamos tomar a expressão em termos do campo elétrico e substituir nela para e .
Para , o módulo de pode ser escrito como
que tem um comportamento linear com a distância .
Para , a área pela qual o campo magnético varia é . Por isso, o módulo do campo elétrico neste caso é
que decresce com o aumento da distância .
Por isso temos o seguinte:
- :
O gráfico que representa corretamente esse comportamento é o do item IV.
Resposta
Portanto, a resposta correta é a letra d).