Considere uma superfície fechada S, com vetor unitário normal apontando para fora. Sabendo que o fluxo de campo elétrico através de S é positivo, considere as afirmativas abaixo:
- Não pode haver partículas de carga negativa no interior de S.
- O campo elétrico deve necessariamente apontar para fora de S em todos os pontos dessa superfície.
- Não pode haver partículas de carga negativa no exterior de S.
São VERDADEIRAS as afirmativas:
- Nenhuma delas.
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
Passo 1
Cara... Antes de tudo, vamos desenhar o que está acontecendo no problema para depois investigarmos a veracidade dos itens, beleza?
O problema nos disse que temos uma superfície fechada qualquer com o vetor normal para fora...
Eu desenhei um cilindro, mas você poderia desenhar qualquer outra superfície fechada, beleza?
Bem... Mas em seguida o enunciado nos disse que o fluxo total do campo elétrico nesse cilindro é positivo. Isto é, o campo elétrico pode entrar e sair de diversas formas ao longo do cilindro, mas a soma de todo mundo tem que necessariamente resultar em um campo total saindo, veja...
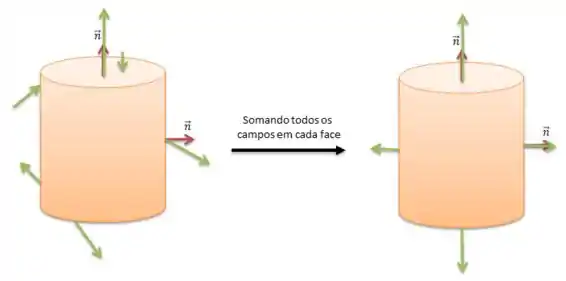
Então, baseado nisso, e também na Lei de Gauss que nos diz que o fluxo do campo elétrico depende do total da carga interna na região fechada ...
Vamos analisar os itens, shall we?
Passo 2
No item ele afirma que não pode haver carga negativa no interior da região .
Ora... Falso! Afinal de contas pode haver carga negativa sim dentro da região . Acontece que o total de cargas dentro da região tem que resultar em carga positiva (só assim teremos um resultado positivo para o fluxo de campo elétrico).
Resumindo no desenho...
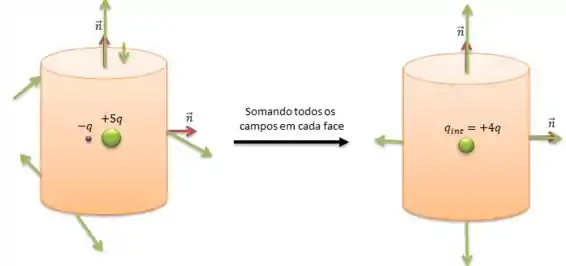
Passo 3
Ora... O item é falso também.
Pelo desenho a gente vê que pode haver em um ponto campo elétrico entrando na região fechada . Só que no total (somando todo mundo) necessariamente deve sair, ou seja, a parte que entra é menor que a parte que sai, saca?
Passo 4
O item também é falso pelo simples motivo de que não importa a carga que está do lado de fora, apenas o total de carga do lado de dentro!
Então pode sim haver cargas negativas do lado de fora da superfície, afinal tanto faz! Ela não interfere no fluxo total do campo elétrico que atravessa a região, saca?
Resposta
Letra A